COMBINATION OF CELLS

INTRODUCTION

In the previous articles, we have seen that how can we combine resistors in series and parallel? and how can we find the equivalent resistance for the same?

Suggested reading – resistors in series and parallel.

But what about cells? Can we combine cells in series and parallel as resistors? Yes! We can also combine it like resistors. The combination of cells in series and parallel is not a complex task. Its combination is similar to that of the resistor.

If anyone knows how to combine resistors in series and parallel, then definitely he can combine cells also. So in this article, we are going to discuss the combination of cells in series and parallel in detail. So stay tuned with us till the end. So let’s start.

Before we start our discussion, let’s first discuss the cells because in this article, mainly we are going to talk about the different arrangements of cells. So we must take knowledge about it.

WHAT IS A CELL?

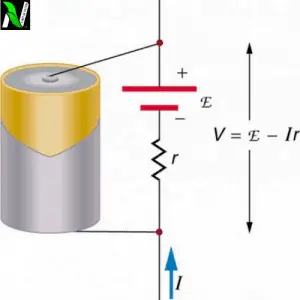
A cell is a single electrical energy source that uses a chemical reaction to produce an electric current. It has two terminals one is the cathode (+ terminal) and the second is the anode (- negative terminal). When electrical devices are connected to it, the current starts flowing from the positive terminal to the negative terminal passing through the device.

A cell is sometimes called an electrochemical cell because it is capable of generating electric current by continuous chemical reactions or it is capable of causing chemical reactions by using electric current.

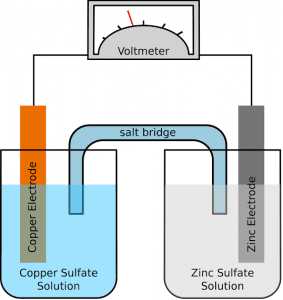
Simply we can say, an electrochemical cell is a device that converts chemical energy to electrical energy or vice versa. So an electrochemical cell that generates electric current by using chemical reactions is called a voltaic cell or Galvanic cell. And those cells which carried out chemical reactions by using electric current via electrolysis are called electrolytic cells. [latexpage]

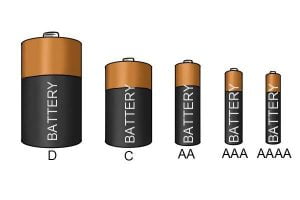
You must have seen finger-like AAA or AA cell, which is widely used in TV remote controls or wall clocks. These cells are the common example of Galvanic cells having an EMF of 1.5V.

When we connect two or more cells in series then it becomes a battery. Basically, there are two ways to combine cells. We can combine two or more cells by series combination or by parallel combination. Let’s discuss these combinations in detail.

CELLS IN SERIES COMBINATION

We know that series means end-to-end connection. When n identical cells each of EMF ε and internal resistance r are connected end to end to the external resistance R in a circuit then this connection of cells is called a series combination of cells. See figure below:

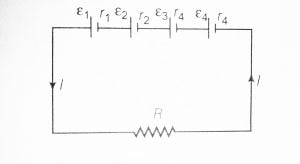
In the series combination, the equivalent EMF of the cells is equal to the sum of their individual EMFs. Let consider a circuit having n cells and each of them having the different value of EMFs, then the equivalent EMFs of the cells in series is given as-
$$\epsilon_{eq}=\epsilon_1+\epsilon_2+\epsilon_3+…+\epsilon_n=n\epsilon$$
We get value nε when each cell has the same value of EMFs.

We know that each cell has some internal resistance r, if we are connecting these cells in series then it means, we are also joining the internal resistance of each cell in series. So equivalent internal resistance of a series combination of cells is equal to the sum of an individual’s internal resistance.

Let consider the same circuit having n cells and each of them having the different value of EMFs and internal resistance, then the equivalent internal resistance of the cells in series is given as-
$$r_{eq}=r_1+r_2+r3+…+r_n=nr$$
We get the value nr when the value of the internal resistance of each cell is the same.
The total resistance of the circuit including total internal resistance (nr) and external resistance (R) is given as-
$$\text{total resistance of the circuit}=nr+R$$
So the value of electric current in the circuit can be given as-
$$I=\frac{n\epsilon}{R+nr}$$
Where n is the number of the cells in series, r is the internal resistance, R is the external resistance, ε is the EMF of the cell and I is electric in the circuit.

DIFFERENT CASES

Case (1). If value of external resistance R is much less than total internal resistance i.e R <<< nr, then $$I=\frac{n\epsilon}{r}$$

Case (2). If value of external resistance is much more than the total internal resistance i.e R >>> nr, then
$$I=\frac{n\epsilon}{R}$$

Case (3). If cells are different EMFs and internal resistance then the value of electric current is-
$$I=\frac{\epsilon_1+\epsilon_2+…}{R+\left(r_1+r_2+…\right)}$$

The maximum current can be drawn from the series combination of the cells if the external resistance R is very high as compared to the total internal resistance of the cells.

CELLS IN PARALLEL COMBINATION

We know that parallel is a way of connection in which all left terminals of cells/resistors are joined together and all the right terminals of cell/resistors are joined together.

In the case of cells, when all the positive terminals of the cells are joined together and similarly all the negative terminals of the cells joined together then we say it is combined in a parallel way.

After joining all the cells in this way, we get finally one positive terminal and one negative terminal and now we can add any load or other external resistance to this terminal to make the circuit complete. See figure below:

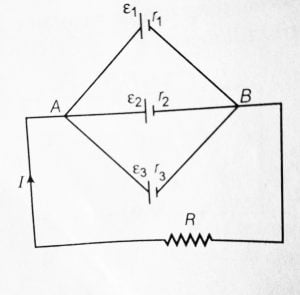
When m cells of each of EMF ε and internal resistance r are connected in parallel so that current passes to the external resistance R, then the cells are said to be connected in parallel.

When we connect cells in parallel, then the equivalent EMF of the combination is equal to the value of the individual EMF of the cell. Same as resistors, when we combine resistors in parallel, then the potential difference at each terminal of the resistor remains the same.

Combining cells in parallel, means we are also combining their internal resistance in parallel. And we know that how to find the equivalent resistance of the resistors when they are in parallel combinations.

The equivalent internal resistance of cells in parallel combination is equal to the sum of the reciprocals of internal resistance of the individual cell.
$$\frac{1}{r_{eq}}=\frac{1}{r_1}+\frac{1}{r_2}+…+\frac{1}{r_m}$$
Where m is number of cells in parallel combination. If internal resistance of all the cells are equal then the equivalent internal resistance is-
$$\frac{1}{r_{eq}}=\frac{1}{r}+\frac{1}{r}+…\text{upto m terms}=\frac{m}{r}$$
$$\text{or}\qquad r_{eq}=\frac{r}{m}$$
So external resistance R and equivalent internal resistance will be series, then the total resistance in the circuit will be-
$$\text{total resistance in the circuit}=R+\frac{r}{m}$$
In parallel combination of the cells, the effective EMF in the circuit is equal to the EMF due to single cell, is because in this type of combination only electrodes of the cells increases but EMF doesn’t.

According to the ohm’s Law, electric current is given as potential difference per resistance. So the value of electric current in the resistance R is given as-
$$I=\frac{\epsilon}{R+\frac{r}{m}}$$

DIFFERENT CASES

Case (1). If R >>> $\displaystyle{\frac{r}{m}}$, then-
$$I=\frac{\epsilon}{R}$$
Case (2). If R <<< $\displaystyle{\frac{r}{m}}$, then-
$$I=\frac{\epsilon}{r/m}=\frac{m\epsilon}{r}$$
Case (3). If cells are of different EMFs and different internal resistance, then-
$$I=\frac{\epsilon}{R+r’}$$
$$\text{Where}\qquad \frac{1}{r’}=\frac{1}{r_1}+\frac{1}{r_2}+\frac{1}{r_3}+…+\frac{1}{r_n}$$

The maximum current can be drawn from the parallel combination of cells, if value of external resistance R is very small as compared to the total internal resistance of the cells.

MIXED GROUPING OF THE CELLS

See the figure below, the way in which cells are connected below is called mixed grouping of the cells. Because in this circuit, n cells in series in one row and m rows of the cells are in parallel.

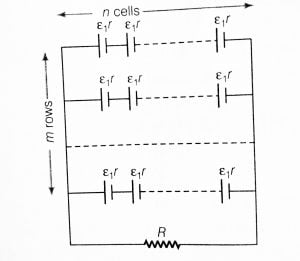
Suppose all the cells in the combination are identical having EMF ε and internal resistance r.

Then, the equivalent EMF of the cells in each row =$n\epsilon$, and the equivalent internal resistance of each row is = $nr$. The total EMF of the whole circuit will be nε because all series cells are also in parallel, so the equivalent of the series will be the effective EMF in the whole circuit.
The total internal resistance of the circuit is-
$$
\frac{1}{r_{eq}}=\frac{1}{nr}+\frac{1}{nr}+…\text{upto m terms}$$
$$\frac{1}{r_{eq}}=\frac{m}{nr}\;\text{or}\;r_{eq}=\frac{nr}{m}$$
$$\text{total resistance of the circuit}=\frac{nr}{m}+R$$
Electric current in the resistance R is given as-
$$\boxed{I=\frac{n\epsilon}{\frac{nr}{m}+R}}$$

So, the maximum current can be drawn from the mixed combination of the cells if the value of external resistance R is equal to the value of the total internal resistance i.e is $\displaystyle{R=\frac{nr}{m}}$

COMBINATION OF TWO CELLS IN SERIES AND PARALLEL

In this section we will see, how can we combine two cells in series and parallel having different EMFs and internal resistance? We will find their equivalent internal resistance and equivalent EMFs and also we will obtain the expression for electric current in the respective circuit.

TWO CELLS IN SERIES

Between the two points A and C, the two cells are said to be connected in series when the negative terminal of one cell is connected to the positive terminal of the second cell. See figure below:

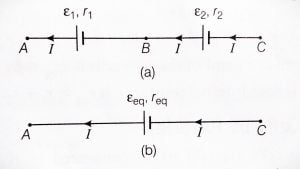
If $\epsilon_1$ and $\epsilon_2$ are the EMFs and $r_1$ and $r_2$ are the internal resistance of the cells which is connected between the points A, B, and C respectively.

If the circuit is closed, then it means cells are sending electric current to the circuit with the magnitude of I. And if $V_A, V_B$, and $V_C$ are the potentials at the point A, B and C then, the potential difference between the negative and positive terminal of the first cell is-
\begin{equation}
V_{AB}=V_A-V_B=\epsilon_1-Ir_1
\end{equation}
Similarly, the potential difference between the positive and negative terminal of the second cell is-
\begin{equation}
V_{BC}=V_B-V_C=\epsilon_2-Ir_2
\end{equation}
But the potential difference between the points A and C of the cells in series combination is-
\begin{equation}
\begin{aligned}
V_{A C} &=V_{A}-V_{C} \\
&=\left(V_{A}-V_{B}\right)+\left(V_{B}-V_{C}\right) \\
&=\left(\varepsilon_{1}-I r_{1}\right)+\left(\varepsilon_{2}-I r_{2}\right) \\
&=\left(\varepsilon_{1}+\varepsilon_{2}\right)-I\left(r_{1}+r_{2}\right)
\end{aligned}
\end{equation}
Equation (3) gives the equivalent cell which we can add in the above circuit in place of these two cells. From thr above equation the equivalent EMF and equivalent internal resistance of the equivalent cell is-
\begin{equation}
V_{AC}=\varepsilon_{eq}-Ir_{eq}
\end{equation}
After comparing equ(3) and equ(4), we get-
\begin{equation}
\begin{aligned}
\varepsilon_{eq}&=\varepsilon_1+\varepsilon_2\\
r_{eq}&=r_1+r_2
\end{aligned}
\end{equation}
We can generalizes this results, if n cells of EMFs $\varepsilon_1, \varepsilon_2, \varepsilon_3,…\varepsilon_n$ and internal resistance $r_1, r_2, r_3,…r_n$ are connected in series then the equivalent EMF $\varepsilon_{eq}$ and equivalent internal resistance $r_{eq}$ can be given as-

\begin{equation}
\boxed{
\begin{aligned}
\varepsilon_{eq}&=\varepsilon_1+ \varepsilon_2+ \varepsilon_3+…+\varepsilon_n\\
r_{eq}&=r_1+ r_2+r_3+…+r_n
\end{aligned}}
\end{equation}
So we can conclude from the above expression that-

• In a series combination of the cells, the equivalent value of the EMFs is equal to the sum of the individual EMFs.
• Similarly, the equivalent internal resistance of the cells is equal to the sum of the individual internal resistance of the cells.

By mistake, if we joined the negative terminal of the first cell to the negative terminal of the second cell between points A and C, see figure below: then-
$$V_{BC}=V_B-V_C=-\varepsilon_2-Ir_2$$
So the equivalent EMF and equivalent internal resistance of such combination is-

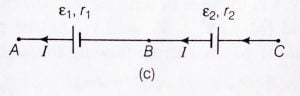
\begin{align*}
\varepsilon_{eq}&=\varepsilon_1-\varepsilon_2\\
r&=r_1+r_2
\end{align*}

TWO CELLS IN PARALLEL

The two cells are said to be connected in parallel between the two points if the positive terminal of each cell is connected to one point and the negative terminal of each cell is connected to the other point. See figure below:

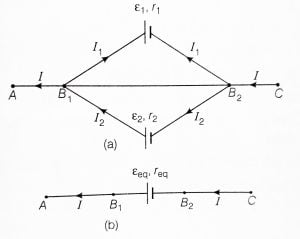
Let $\varepsilon_1$ and $\varepsilon_2$ are the EMF of the cells and $r_1$ and $r_2$ be the internal resistance of the cells in parallel combination respectively. Let $I_1$ and $I_2$ are the current flowing from the cells towards the point $B_1$ and I is the electric current flowing out of the point $B_1$. Then the total electric current in the circuit is given as-
\begin{equation}
I_1+I_2=I
\end{equation}
If $V_{B_1}$ and $V_{B_2}$ be the potentials at point $B_1$ and $B_2$ and let V is the potential difference between the terminals of first cell and between the terminals of the second cell, here the potential difference across the terminals of each cells is same because it it joined in parallel. Then for the first cell-
\begin{equation}
\begin{aligned}
V&= V_{B_1}- V_{B_2}=\varepsilon_1-I_1r_1\\
\text{or}\qquad I_1&=\frac{\varepsilon_1-V}{r_1}
\end{aligned}
\end{equation}
Similarly, for the second cell-
\begin{equation}
\begin{aligned}
V&= V_{B_1}- V_{B_2}=\varepsilon_2-I_2r_2\\
\text{or}\qquad I_2&=\frac{\varepsilon_2-V}{r_2}
\end{aligned}
\end{equation}
Now put the values of these current in the equ(7), we get-
\begin{equation}
\begin{aligned}
I&=\left(\frac{\varepsilon_1-V}{r_1}\right)+\left(\frac{\varepsilon_2-V}{r_2}\right)\\
&=\left(\frac{\varepsilon_1}{r_1}+\frac{\varepsilon_2}{r_2}\right)-V\left(\frac{1}{r_1}-\frac{1}{r_2}\right)\\
&=\frac{\varepsilon_1r_1+\varepsilon_2r_2}{r_1r_2}-V\left(\frac{r_1+r_2}{r_1r_2}\right)\\
V&=\frac{\varepsilon_1r_1+\varepsilon_2r_2}{r_1+r_2}-\frac{Ir_1r_2}{r_1+r_2}
\end{aligned}
\end{equation}
The above equation gives the idea of an equivalent cell if we want to replace the parallel combination of these two cells and want to connect a single cell. Then the EMF and internal resistance of the single-cell must be equal to the equivalent EMF and equivalent internal resistance of the cells which is parallelly combined.

The relation between potential difference V, equivalent EMF, and equivalent internal resistance of the new single cell can be given as-
$$V=\varepsilon_{eq}-Ir_{eq}$$
Comparing these equivalents with the equ (10), we get-
\begin{equation}
\begin{aligned}
\varepsilon_{eq}&=\frac{\varepsilon_1r_1+\varepsilon_2r_2}{r_1+r_2}\\
r_{eq}&=\frac{r_1r_2}{r_1+r_2}\\
\text{or}\qquad \frac{1}{r_{eq}}&=\frac{r_1+r_2}{r_1r_2}=\frac{1}{r_1}+\frac{1}{r_2}
\end{aligned}
\end{equation}
If we divide equivalent EMF value by the equivalent internal resistance value then-
\begin{equation}
\frac{\varepsilon_{eq}}{r_{eq}}=\frac{\varepsilon_1r_1+\varepsilon_2r_2}{r_{1}r_{2}}= \frac{\varepsilon_1}{r_1}+\frac{\varepsilon_2}{r_2}
\end{equation}
So in general we can say if there are n cells having EMFs $\varepsilon_1, \varepsilon_2,…,\varepsilon_n$ and internal resistance $r_1, r_2,…,r_n$ are connected in parallel then their equivalent EMF and internal resistance is given as-
\begin{align*}
\frac{1}{r_{eq}}&=\frac{1}{r_{1}}+\frac{1}{r_{2}}+…+\frac{1}{r_{n}}\\
\frac{\varepsilon_{eq}}{r_{eq}}&=\frac{\varepsilon_1}{r_1}+\frac{\varepsilon_2}{r_2}+…+\frac{\varepsilon_n}{r_n}
\end{align*}

If two cells are connected in parallel but they have the same EMF and internal resistance then their equivalent EMF and equivalent internal resistance are given as-
$$\varepsilon_{eq}=\frac{\varepsilon r+\varepsilon r}{r+r}=\varepsilon$$
$$\frac{1}{r_{eq}}=\frac{1}{r}+\frac{1}{r}=\frac{2}{r}\; \text{or}\;r_{eq}=\frac{r}{2}$$

If two or more cells are connected in parallel combination, then we can conclude that-

• If the cells having the same EMF and are combined into the parallel then the equivalent EMF of the combination is equal to the EMF of the individual cell.
• If the cell having the same internal resistance and they are combined into parallel then the reciprocal of their equivalent internal resistance is equal to the sum of reciprocal of their individual internal resistance.

For more such interesting and useful content stay tuned with Laws Of Nature.