COMBINATION OF RESISTORS

In the previous articles, we have discussed Resistors? and their various types and color-coding of the Resistors, and how to read Resistor’s color codes.

But in this article, we will discuss the combination of the resistors in any electrical circuit. In this article, We will see what is the series combination of resistors? What is the parallel combination of resistors? what is a mixed combination of resistors, and many more related topics? So stay tuned with us till the end.

Going further, let’s take a brief note about what is Resistors?

WHAT IS A RESISTOR?

A resistor is a passive device that lowers the flow of electric current in an electric circuit. Every resistor has its own abilities to resist the electric current. This ability is sometimes called resistance of the Resistors.

There are various types of resistors available in the market based on their applications and their needs.

Suggested reading – Resistors and it’s types

Resistors are widely being used in electrical engineering. All electrical equipment which do you see like charger, television, smartphone, playing remote control car, electric fan or everything which runs on electricity have Resistors on their motherboard. You can’t make any desirable electrical gadgets without the use of Resistors.[latexpage]

WHY DO WE NEED TO COMBINE RESISTORS?

In any electrical motherboard there can be more than one Resistors, which will be combined with the other Resistors in series or parallel to provide a particular or equivalent value of resistance, which is used to give a desirable output by the gadgets.

For example: Assume you have five Resistors and each resistor has a different value of resistance then how will combine these Resistors to give a fixed value of resistance let say R. To find this fixed particular value you have to combine some Resistors in series or some are in parallel. So a combination in which both series and parallel arrangements are involved is called a mixed combination.

There are various reasons or points of view due to which we have to combine Resistors in series and parallel. Some points of views are –

• Less availability of high resistance Resistors in the market. For example: If you need a 100Ω Resistor then it is a very low chance that you will get it.
• Keep the size of the circuit small. For example: Let’s assume, luckily you have found 100Ω Resistors but its size would be large. And it will consume more power. So it is easier to buy small Resistors and Combined them in such a way that they will give same resistance.
• To save electricity, small Resistors will consume less power but large Resistors will consume more power and will get hot.
• When you combine small Resistors in long branched chains having parallel or series combinations, keep the motherboard light. It will always light in weight in comparison to the other large heavy Resistors.

So due to this reason, we need to combine Resistors in series and parallel. And we will see some more advantages of combining Resistors in series and parallel in the below sections.

RESISTORS IN SERIES COMBINATION

Series means end-to-end connection. When two or more Resistors are connected to each other by the end-to-end method then this type of method of connection is called the series combination of resistors.

The following figure shows the series combination of resistors. in the following figure, you will see that all the resistors are connected to the other resistors by head to tail or end to end.

In the series combination of resistors. You will see that there is only one path for the electric current, which means the electric current has to travel in only one direction by passing through each resistor.

But if it passes through each resistor then it means every resistor has contained the same amount of electric current. but what about the potential difference, does it also same for each resistor? no, this is not the same as electric current, the potential difference for each resistor has a different value. so why is it different?

According to the ohm law – if I current is flowing through an electrical circuit and if the circuit has a resistance of R then the potential difference is given by V = IR.

So in the above circuit, we have both resistance and current then we can easily find the value of potential difference which is supplying through the circuit.

In the above figure, we have three different resistors which mean they have three different value of resistance i.e $R_1$, $R_2$, and $R_3$. if they have three different values of resistance then they have three different values of potential difference. The potential associated with each resistor is given as-
\begin{align*}
V_1&=IR_1\\
V_2&=IR_2\\
V_3&=IR_3
\end{align*}

EQUIVALENT RESISTANCE OF SERIES COMBINATION

Let V is the potential difference, I is the electric current and R is the resistance of the whole circuit then according to the ohm law, the relation between them is V = IR.

But we have seen that circuit has three different values of the potential difference. These three potential difference is the parts of the main potential difference if we sum it algebraically then we will get the main potential difference.
$$V=V_1+V_2+V_3$$
$$V=IR_1+IR_2+IR_3$$
Put the value of V in the above equation, after putting we get-
\begin{align*}
IR&=IR_1+IR_2+IR_3\\
IR&=I\left(R_1+R_2+R_3\right)\\
R&=R_1+R_2+R_3
\end{align*}

This R is called the total resistance or equivalent resistance of the Resistors in a series combination.

IMPORTANT POINTS RELATED TO SERIES COMBINATION

Some important points related to the series combination of the resistors

• It is an end-to-end connection of the Resistors.
• The same amount of electric current flows through each resistor.
• Current through the Resistors is directly proportional to the resistance of the resistors.
• The potential difference for each resistor is different.
• Some of all the potential difference of each resistor is equal to the voltage of the main power source.
• The equivalent resistance of the Resistors is equal to the sum of the individual resistances of the Resistor.
• Equivalent resistance gives the larger value of resistance among all the resistance of the resistors in the circuit. For example: let a circuit has three Resistors having resistance value 2Ω, 4Ω and 6Ω, then the equivalent resistance is 12Ω which greater than all the resistance involved.
• Consume more power

RESISTORS IN PARALLEL COMBINATION

The parallel combination of Resistors is different from the series combination of Resistors.

Series is an end-to-end connection but the parallel combination is a method of connection in which left terminals of all the Resistors are joined together and similarly right terminals are joined together. See figure below:

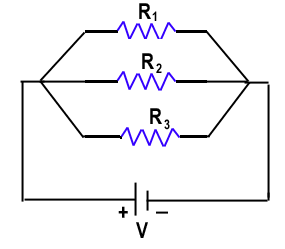
The parallel combination makes branching of the Resistor due to this various different path created.

When current starts flowing from the positive terminal towards the negative terminal then the pathway is divided into various smaller currents but when it meets again at the joint then they add up to give the original current.

Due to this division of electric current, each resistor has a different value of current flowing. But each of them has the same potential difference as the source because they are connected to the same power source. See figure below.

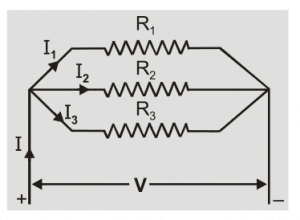
EQUIVALENT RESISTANCE OF PARALLEL COMBINATION

Let’s take a circuit having total resistance R, potential difference V and electric current I. You can take the above figure for reference. Then according to ohm’s Law V = IR, then electric current can be given as-
$$I=\frac{V}{R}$$
The total current in the circuit can be given as-
$$
I=I_1+I_2+I_3
$$
If I can be written as $\frac{V}{R}$ then similarly, we can write-
\begin{align*}
I_1&=\frac{V}{R_1}\\
I_2&=\frac{V}{R_2}\\
I_3&=\frac{V}{R_3}
\end{align*}
Put these values in the above current equation, we get-
$$
I=\frac{V}{R}=\frac{V}{R_1}+\frac{V}{R_2}+\frac{V}{R_3}
$$
Cancelling V from both side we get-
$$
\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}
$$
Rewrite this formula as follows-
$$
\frac{1}{R_eq}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}
$$
This $R_eq$ is called the total or equivalent resistance of the parallel combination of the resistors.

IMPORTANT POINTS RELATED TO PARALLEL COMBINATION

Some important points related to the parallel combination of resistors.

• In parallel combination left terminals of all Resistors are joined together and right terminals are also joined as left.
• Current through each resistor is inversely proportional to the resistance of the Resistors.
• Original current divided into several small currents when they entered into the branch created during parallel combination. See figure above.
• Output current is always equal to the input current. If the positive terminal leaves 1A of current then after several divisions into the branches, it entered as 1A in the negative terminal.
• The total current in the circuit is equal to the sum of all the currents in an individual Resistor.
• The potential difference remains the same across all the Resistors.
• In parallel combination, the equivalent resistance is the smallest among all the Resistors involved.
• Consume less power