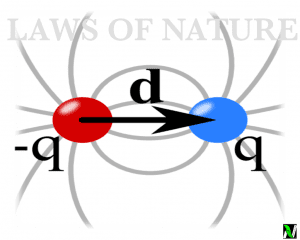
Superposition principles of electrostatic force
The topic which we are going to talk about today is one of the important topics of electrostatic. Today we are going to talk about the principle of superposition of electrostatic force. This principle is very important and widely used in acoustic, wave optics, and current electricity and engineering.
So it becomes very important for us to understand this principle and learn about this. For understanding the basic concept of superposition principles. Let’s consider a situation.
Superposition principle
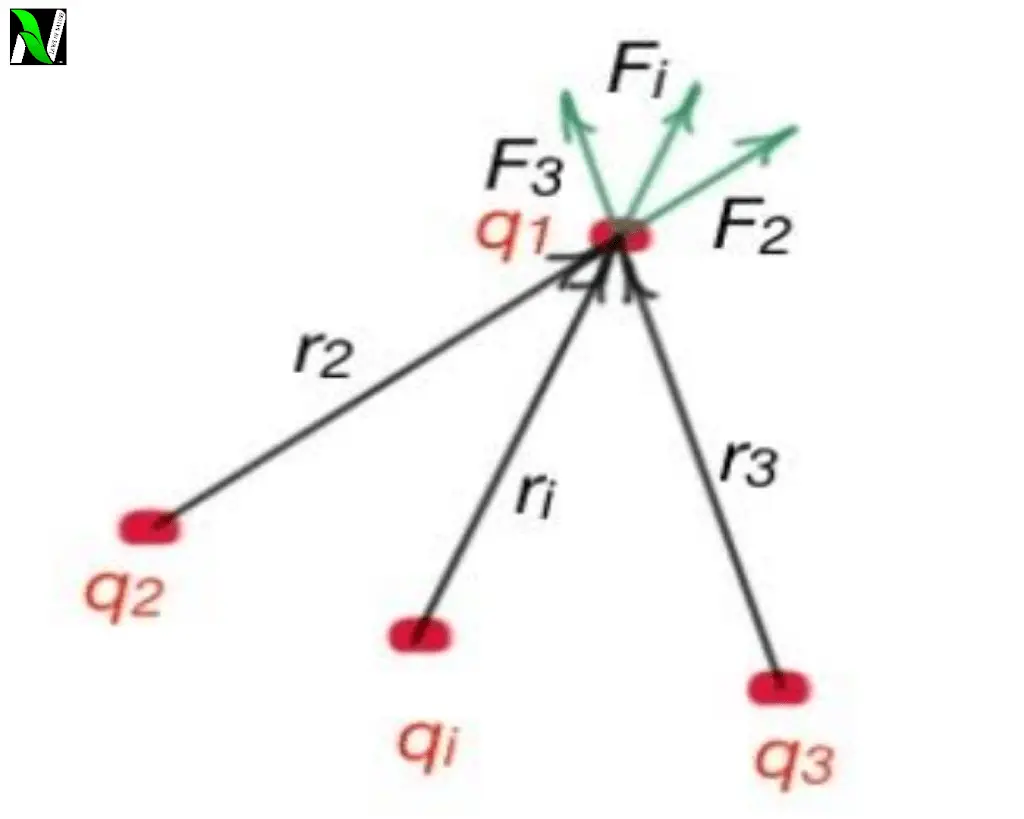
Think of a charge $q_1$ in the open space, which is surrounded by a system of n stationary charges at different distances. The charges which surround the charge $q_1$ are $q_2, q_3 …..$ and $q_n$. We know that these electrical charges exert electrostatic force on each other, which can be measured by the coulomb’s Law. But what is the electrostatic force on the charge $q_1$ due to all charges? This is the situation where the superposition principle comes into play.
Superposition principles – According to this principle, force on any charge is the vector sum of all the forces on that charge due to the presence of other charges at a time. The main feature of this principle is that the individual charge remains unaffected due to the presence of other charges.
The charge which we have thought of in the open space i.e the charge $q_1$, will experiences force from the other charges i.e $q_2, q_3 …$, and $q_n$.
The force experienced by the charge $q_1$ due to other charges $q_2, q_3…$ and $q_n$ is given as – $F_{12}, F_{13} …. \text{and}\; F_{1n} \qquad…(1)$
According to the superposition principle, the total force experienced by the charge $q_1$ is given as – $$F = F_{12} + F_{13} + …. + F_{1n}$$ If the distance between the charge $q_1$ and $q_2$ is denoted by $r_{12}$ and $r_{21}$ is the unit vector from the charge $q_2$ and $q_1$, then $$F_{12} = \frac{q_1 q_2}{4\pi\epsilon_0 r_{12}^2}r_{21}$$
Similarly, the force on the charge $q_1$ due to other charges is – $$\begin{align}F_{13}& = \frac{q_1 q_3}{4\pi\epsilon_0 r_{13}^2}r_{31}\\ F_{1n} &= \frac{q_1 q_n}{4\pi\epsilon_0 r_{1n}^2}r_{n1}\end{align}$$ Putting these force in the equation (1) , then we get –
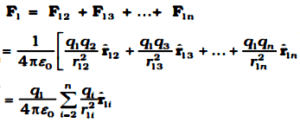
Watch the video for more reference
Stay tuned with Laws Of Nature for more useful and interesting content.