In this short piece of article, we will derive an expression for the root mean square value of alternating current for a full cycle, so let’s get started…
Root mean square (RMS) or virtual or effective value of AC
It is defined as the value of a direct current which produces the same heating effect in the given resistor as is produced by the given alternating current when passed for the same time. It is denoted as $I_{rms},\; I_v\;\text{or}\;I_{eff}$.
RMS value of alternating current for a full cycle
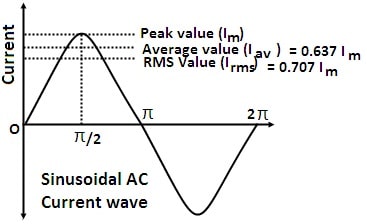
Suppose an alternating current $I=I_0\sin\omega t$ is passed through a circuit of resistance $R$. Then, the amount of heat produced in small time $dt$ will be
$$ d H=I^{2} R d t $$ If $T$ is the time period of AC then heat produced in one complete cycle will be $$ H=\int_{0}^{T} I^{2} R d t $$ Let $I_{\text {eff }}$ be the effective value of AC Then heat produced in time $T$ must be
Read Also
| $$ \therefore \quad I_{e f f}^{2} R T=\int_{0}^{T} I^{2} R d t \text { or } I_{e f f}^{2}=\frac{1}{T} \int_{0}^{T} I^{2} d t $$ |
But, $\displaystyle{\frac{1}{T} \int_{0}^{T} I^{2} d t}$ is the mean of the squares of the instantaneous values of AC over one complete cycle, hence the effective or virtual value of AC equals its root mean square value, i.e., $$ I_{e f f}=I_{r m s}=\sqrt{\frac{1}{T} \int_{0}^{T} I^{2} d t} $$ Now
| $$ \begin{aligned} \int_{0}^{T} I^{2} d t &=\int_{0}^{T} I_{0}^{2} \sin ^{2} \omega t d t \\ &=I_{0}{ }^{2} \int_{0}^{T} \frac{1-\cos 2 \omega t}{2} d t \\ &=\frac{I_{0}{ }^{2}}{2}\left[t-\frac{\sin 2 \omega t}{2 \omega}\right]_{0}^{T} \\ &=\frac{I_{0}^{2}}{2}\left[(T-0)-\frac{1}{2 \omega} \mid \sin \frac{4 \pi}{T} t\mid_{0}^{T}\right] \\ &=\frac{I_{0}{ }^{2}}{2}\left[T-\frac{1}{2 \omega}(\sin 4 \pi-\sin 0)\right] \\ &=\frac{I_{0}{ }^{2}}{2}[\mathrm{~T}-0]=\frac{I_{0}{ }^{2} T}{2} \\ \therefore \quad I_{e f f} \text { or } I_{r m s} &=\sqrt{\frac{1}{T} \cdot \frac{I_{0}{ }^{2} T}{2}} \\ \text { or } \quad I_{e f f} \text { or } I_{r m s} &=\frac{1}{\sqrt{2}} I_{0}=0.707 I_{0} \end{aligned} $$ |
Thus the effective or RMS value of an AC is $\frac{1}{\sqrt{2}}$ times its peak value.
Read Also
Frequently Asked Questions – FAQs
What is the value of RMS value?
The RMS value of a sinusoidal current (or any time-varying current) is defined as the value of a direct current which produces the same heating effect in the given resistor as is produced by the given alternating current when passed for the same time.
What is the peak value of AC?
The peak value of the alternating current is √2 times the root mean square value of the alternating current. i.e $$I_0=\sqrt{2}I_{rms}$$
What is the RMS value of the AC formula?
the effective or RMS value of an AC is $\frac{1}{\sqrt{2}}$ times its peak value. i.e $$I_{r m s} =\frac{1}{\sqrt{2}} I_{0}=0.707 I_{0}$$
What is the mean value of AC?
The mean value of an alternating current is the total charge flown for one complete cycle divided by the time taken to complete the cycle i.e. time period T. The magnitude of an alternating current changes from time to time and its direction also reverses after every half cycle.
Stay tuned with Laws Of Nature for more useful and interesting content.