ELECTRIC POTENTIAL DUE TO SYSTEM OF CHARGES

In this article we are going to derive an expression for electric potential due to system of charges. So keep reading…

DERIVATION FOR THE EXPRESSION

$latexpage$
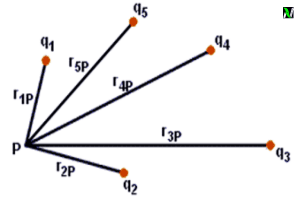
Let’s consider $\displaystyle{q_1, q_2, q_3, … q_n}$ are the point charges which are located at the distances $\displaystyle{r_1, r_2, r_3 ,… r_n}$ respectively from a point P. See figure above. Now electric potential due to charge $q_1$ is-
$$V_1=\frac{1}{4\pi\epsilon_{0}}\frac{q_1}{r_1}$$
Similarly, electric potential due to others charges.
$$\begin{align*} V_{2}&=\frac{1}{4\pi\epsilon_{0}}\frac{q_2}{r_2}\\ V_{3}&=\frac{1}{4\pi\epsilon_{0}}\frac{q_3}{r_3}\\ V_{n}&=\frac{1}{4\pi\epsilon_{0}}\frac{q_n}{r_n} \end{align*}$$
By using superposition principle, we can obtain resultant value of electric potential at point P due to total charge configuration as algebraic sum of all the electric potential due to individuals charges.
$$\begin{align*} V&=V_1+V_2+V_3+…+V_n\\ V&=\frac{1}{4\pi\epsilon_{0}}\frac{q_1}{r_1}+\frac{1}{4\pi\epsilon_{0}}\frac{q_2}{r_2}\\ &+\frac{1}{4\pi\epsilon_{0}}\frac{q_3}{r_3}+…+\frac{1}{4\pi\epsilon_{0}}\frac{q_n}{r_n} \end{align*}$$
Now taking common $\displaystyle{\frac{1}{4\pi\epsilon_{0}}}$ from above equation, then we get-
$$V=\frac{1}{4\pi\epsilon_{0}}\left[\frac{q_1}{r_1}+\frac{q_2}{r_2}+\frac{q_3}{r_3}+…+\frac{q_n}{r_n}\right]$$
$$\implies \boxed{V=\frac{1}{4\pi\epsilon_{0}}\sum_{i=1}^{n}\frac{q_i}{r_i}}$$
The net electric potential due to the multiple charges at the point P is equal to the algebraic sum of all the potential due to individuals charges. Mathematically it is expressed as-
$$V_{net}=\sum_{i=1}^{n}V_i$$