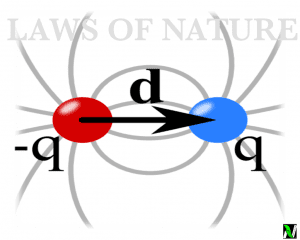
Coulomb’s law
Coulomb’s Law which is also called inverse square law is the experimental law of physics, which quantify the electrical force between the two static electrical charges, which are separated by some distance r.
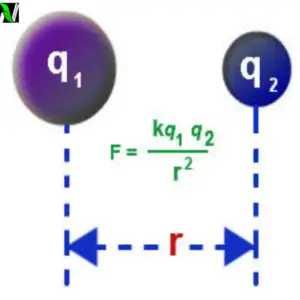
The force between the two static electrical charges is called electrostatic force or coulomb’s force. This law was first published in 1785 by the French physicist Charles Augustin de coulomb. Coulomb’s Law is the first step in the development of the theory of electromagnetism. Watch the practical video of coulomb’s Law.
In this section, we will discuss the coulomb’s Law in detail so tune with us till the end.
Coulomb’s law statement
Coulomb performed various experiments to find the force between the two stationary electrical charges. After a successful experiment, Charles Augustin de coulomb established the following law known as coulomb’s Law.
Coulomb’s law statement: The magnitude of the electrostatic force between the two stationary electrical point charges which is separated by the distance $r$ is directly proportional to the product of their charges and inversely proportional to the square of the distance between them.
Mathematically it is given as – \begin{aligned}F& \propto q_1q_2\\ F& \propto \frac{1}{r^2}\\ F &\propto \frac{q_1q_2}{r^2}\\ \text{And, therefore} \quad F &= \frac{Kq_1q_2}{r^2}\end{aligned}
Key features of coulomb’s law
- This law is applicable only for points charges.
- K is called the proportionality constant and in a vacuum, it is expressed as $\frac{1}{4\pi\epsilon_0}$. Where $\epsilon_0$ is called the permittivity of the free space. And its numerical value is $8.85\times10^{-12} C^2N^{-1}m^{-2}$. Any medium other than vacuum is expressed as $\frac{1}{4\pi\epsilon}$, where $\epsilon$ is called the absolute permittivity of the medium.
- The ratio of $\frac{\epsilon}{\epsilon_0}$ is $\epsilon r$ called the relative permittivity of the medium or dielectric constant of the medium and also denoted as $K$. It is a dimensionless quantity. $$\frac{\epsilon}{\epsilon_0} = \epsilon r = K$$
- The value of relative permittivity $\epsilon r$ varies from 1 to $\infty$, for vacuum, it is 1 and for air, it is nearly equal to 1 and we take 1 for simplicity in calculations, and for metals, it is $\infty$.
- If any charge is placed in the medium having relative permittivity $\epsilon r$ then the electrostatic force between them is $\frac{1}{4\pi\epsilon_0}\cdot\frac{q_1q_2}{r^2}$
- The value of $\frac{1}{4\pi\epsilon_0}$ is $9\times10^{9}Nm^2C^{-2}$.
- The force between the two-point charges always acts along the line joining these two points charges. This force is equal in magnitude but opposite in directions, irrespective of the medium in which they are placed.
- The electrostatic force is conservative in nature i.e the work done by the electrostatic force to move a charge in a close loop of any shape is zero.
- This electrostatic force is a central force, in the absence of other external forces, the angular momentum of one particle with respect to the other particle ( in two particles system) is conserved.
- Coulomb’s Law is analogous to the gravitational Law because both are inverse-square laws. $$\begin{aligned}F(g) &= \frac{Gm_1m_2}{r^2}\\ F(e)& = \frac{Kq_1q_2}{r^2}\end{aligned}$$ Where $G = 6.67\times10^{-11}Nm^2kg^{-2} \text{and}\; K = \frac{1}{4\pi\epsilon_0}\; \text{is}\; 9\times10^9Nm^2C^{-2}$ After comparing both forces we get $F(e) = 10^{39}F(g)$This electrostatic force can be attractive or repulsive on the basis of the nature of the charge.
- If both charges are positive/negative then force is repulsive if they are unlike then the force is attractive.
Read Also
Coulomb’s law in vector form
Let’s take two points charges $q_1$ and $q_2$ which are placed at point $A$ and point $B$ as shown in the following figure.
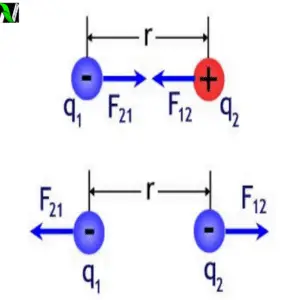
According to coulomb’s Law, the magnitude of the force on $q_1$ due to $q_2$ and the magnitude of the force on $q_2$ due to $q_1$ is given by –
$$|F_{12}| = |F_{21}| = \frac{q_1q_2}{4\pi\epsilon_0\cdot r^2}$$
Now if $r_{12}$ is a unit vector pointing from $q_1$ to $q_2$ and $r_{21}$ is the unit vector pointing from $q_2$ to $q_1$ then the force is –
$$F_{12} = \left(\frac{q_1q_2}{4\pi\epsilon_0\cdot r^2}\right)\;r_{21}$$
$F_{12}$, is the force applied from $q_2$ to $q_1$ along with unit vector $r_{21}$.
$$F_{21} = \left(\frac{q_1q_2}{4\pi\epsilon_0\cdot r^2}\right)\;r_{12}$$
$F_{12}$ , is the force applied from $q_1$ to $q_2$ along unit vector $r_{12}$.
From this, we can conclude that the unit vector $r_{21}$ is opposite to the unit vector $r_{12}$.
$$r_{21} = – r_{12}$$
Then, the second equation becomes –
$$F_{12} = -\left(\frac{q_1q_2}{4\pi\epsilon_0\cdot r^2}\;r_{12}\right)$$
$\left(\frac{q_1q_2}{4\pi\epsilon_0\cdot r^2}\;r_{12}\right)$, this force is equal to $F_{21}$, now the equation becomes – $$F_{12} = – F_{21}$$
This force is equal in magnitude but opposite in directions and this is the same as Newton’s third law.
Watch this video for more reference.
Stay tuned with Laws Of Nature for more useful and interesting content.