Welcome to Laws Of Nature, the most loved academic science site on the internet ever

Let’s Get Into
Featured Science Articles
- Concave mirror and convex mirror: Image formation and characteristicsMirrors are objects that reflect almost all of the light… Read more: Concave mirror and convex mirror: Image formation and characteristics
- Rules for drawing ray diagrams for spherical mirrorsThis short article will teach us the rules for drawing… Read more: Rules for drawing ray diagrams for spherical mirrors
- Derive relation between focal length and radius of curvatureIn this short article, we will derive a relationship between… Read more: Derive relation between focal length and radius of curvature
- Cartesian sign convention for spherical mirrorsIn this short piece of article, we will discuss the… Read more: Cartesian sign convention for spherical mirrors
- Spherical mirrors: definition, types, and terminologiesSpherical mirrors are mirrors that have a curved reflecting surface,… Read more: Spherical mirrors: definition, types, and terminologies
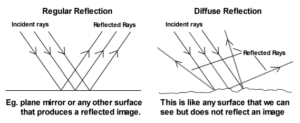
- Reflection of light class 12: definition and typesReflection of light Reflection of light: The bouncing back of… Read more: Reflection of light class 12: definition and types
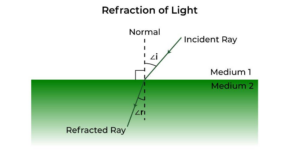
- Behaviour of light at the interface of two mediaWhen light encounters the interface between two different media, such… Read more: Behaviour of light at the interface of two media
- Optics: definition, types, and applications, class 12Optics is a branch of physics that deals with the… Read more: Optics: definition, types, and applications, class 12
- Black body: definition, laws, effects, and propertiesIn physics, a black body or blackbody refers to an… Read more: Black body: definition, laws, effects, and properties
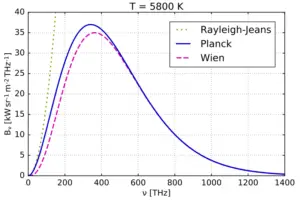
- Rayleigh-Jeans Law: statement, and formula derivationThe Rayleigh-Jeans Law, also known as the Rayleigh-Jeans Formula or… Read more: Rayleigh-Jeans Law: statement, and formula derivation
- Preparation of the soil: class 8The preparation of soil is the first step before growing… Read more: Preparation of the soil: class 8
- Good agricultural practices, class – 8Good agricultural practices (GAPs) are essential for sustainable and productive… Read more: Good agricultural practices, class – 8
- What are crops? & their types, Class 8Crops are plants cultivated by humans for food, fiber, or… Read more: What are crops? & their types, Class 8
- Crop production and management – class 8All living organisms require food for survival and growth. The… Read more: Crop production and management – class 8
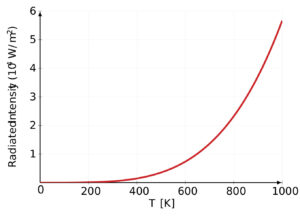
- Stefan-Boltzmann law: statement, constant & formula derivationThe Stefan-Boltzmann Law, also known as Stefan’s law, is a… Read more: Stefan-Boltzmann law: statement, constant & formula derivation
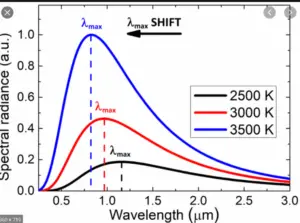
- Wien’s displacement law: statement, formula derivation, & examplesThe Wien’s Displacement Law, formulated by the German physicist Wilhelm… Read more: Wien’s displacement law: statement, formula derivation, & examples