Today we are going to talk about the concept of venturimeter. This device is the application of the Bernoulli principle. This is a very important device that is based on the laws of hydrodynamics.
This device measures the flow speed of incompressible fluid which are flowing through the pipe of different cross-sectional area. This device is also called a flow meter or venturi tube.

This device consists of a horizontal tube or pipe with having a wider opening of cross-sectional area A1 and a narrow neck of cross-section A2, these two regions of the horizontal pipe are connected to a manometer which contains a liquid of density σ. At the wider opening, the velocity of the fluid is v1 and pressure p1 and at the narrower opening the velocity of the fluid is v2 and fluid pressure is p2. And the density of fluid that is flowing through the pipe is ρ. For reference see the diagram below:[latexpage]

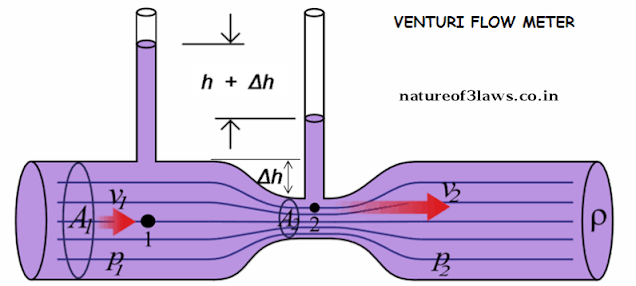
Now we are going to derive the formula for the speed of the fluid, which is flowing through the tube or pipe.

DERIVATION FOR FLOW RATE

If the fluid is flowing through the tube then according to the equation of continuity, we get-
$$A_1v_1 = A_2v_2 Or   \left(\frac{A_1}{A_2}\right) = \left(\frac{v2}{v1}\right)$$
Now using Bernoulli principle for horizontal flow of liquid in the pipe with density ρ.
$$p_1 + \frac{1}{2}\rho v_1^2 = p_2 + \frac{1}{2}\rho v_2^2$$
Then we get-
$$p_1 – p_2 =  \frac{1}{2}\rho\left[v_2^2 -v_1^2\right]$$
Taking common v1^2 then we get-
$$p_1 – p_2 = \frac{1}{2}\rho v_1^2\left[\frac{v_2^2}{v_1^2} -1\right]$$
We know that
$$\frac{v_2^2}{v_1^2} = \frac{A_1}{A_2}$$
If $\displaystyle{\frac{v_2}{v_1}}$ get squared then $\displaystyle{\frac{A_1}{A_2}}$ also get squared.
Then equation becomes-
$$p_1 – p_2 = \frac{1}{2}\rho v_1^2\left[\frac{A_1^2}{A_2^2} -1\right]$$
This pressure difference in the pipe also creates a difference in height in the liquid which are filled in the manometer. So the difference in height h of two arms of the manometer measures the pressure difference, which is given as.
$$p_1 – p_2 = \sigma gh$$
So putting σgh in the above equation in place of $p_1 – p_2$ then,
$$\sigma gh = \frac{1}{2}\rho v_1^2\left[\frac{A_1^2}{A_2^2} -1\right]$$
So from the above equation, the velocity of the fluid is-
$$v_1 = \sqrt{\left(\frac{2h\sigma g}{\rho}\right)}\times\left[\frac{A_1^2}{A_2^2} -1\right]^{\frac{-1}{2}}$$
It is the speed of liquid in the wider opening. Then the volume of the liquid flowing per second through the wider opening is given as follows-
According to the equation of continuity $\displaystyle{V = A_1v_1}$ then putting the value of v1, we get-
$$A_1v_1 = A_1\sqrt{\left(\frac{2h\sigma g}{\rho}\right)}\times\left[\frac{A_1^2}{A_2^2} -1\right]^{\frac{-1}{2}}$$
On simplifying we get-
$$V = A_1A_2\sqrt{\left[\frac{2h\sigma g}{\rho(A_1^2 – A_2^2)}\right]}$$
And we know that hσg is equal to the $p_1 -p_2$
Then after putting the value of σgh in the above volume equation, then we get the final formula for volume flowing per second in the tube.
$$V = A_1A_2\sqrt{\left[\frac{2h\sigma g}{\rho(A_1^2 – A_2^2)}\right]}$$

Watch this video for reference.