Poiseuille’s Law: An overview

So today in today’s article, we are going to talk about a very important and interesting concept of hydrodynamics, that Poiseuille‘s law. So going further it is necessary to understand the underlying concept of poiseuillie’s law in the very simplest form.

The basic underlying concept is that in poiseuillie’s laws, the fluid motion should be streamlined throughout the pipe.

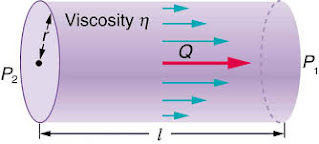
Now, you have known the basic underlying concept of Poiseuille’s laws, So let’s get started…

We are starting the concept with a question, In what manner a viscous fluid flows through a cylindrical pipe? In any cylindrical pipe, when viscous fluid flows they follow a convex meniscus, but why? It is because we know that a streamlined fluid has several streams of fluid.

Some streams are near the wall of the pipe and some stream is far from the wall, In the cylindrical pipe, the longest distance from the wall is to the center of the pipe. And we know that the pipe is cylindrical then the shape of water which is flowing through it, must be in the shape of a cylinder.

Then we can conclude that every fluid lamina in the pipe is in the shape of a cylinder. There are infinite laminae between the center of the pipe and its wall. And as fluid starts flowing through the pipe then friction also creates between the wall of the pipe and the lamina which is nearer to it. And this friction opposes the velocity of the fluid, and at the wall velocity of the fluid is taken as zero, because at this point maximum friction is applied.

Due to this friction opposing forces are generated and this force is termed laminar force or viscous force. And in the pipe each lamina opposes the velocity of the other’s lamina, the first lamina opposes the second lamina, and the second opposes the third, and so on.

And this opposition started from the wall, so the stream which is nearer to the wall has minimum velocity, and as distance increases from the wall then the velocity of the fluid also increases and becomes maximum at the center, which means its velocity is affected by the change of radius $r$ and same occurred from the other sides of the wall, so this form the convex meniscus of the fluid in the pipe.

And this is not only for the cylindrical body, this laminar flow is held in all types of the body in which fluid is flowing. This gives a convex form as given below.

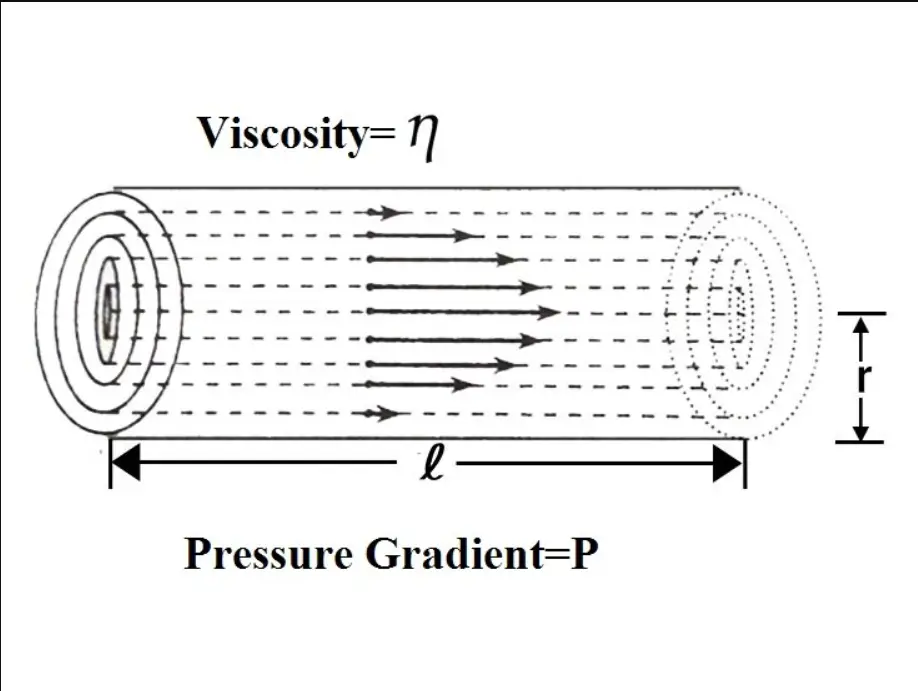
Poiseuille’s Law: Basics

First of all, we have to know that Poiseuille’s law measure what? Poiseuille’s law measure only the rate of flow of volume of fluid per second in the pipe. Going further let’s give a sight at what factors can flow rate of volume depends on.

Factors on which flow rates depend

1. If we think little then we observe that the flow rate depends directly on the pressure difference across the pipe, because if the pressure difference is small the flow of fluid become slow, but if the pressure difference is large then the flow rate increases, we have all seen it in daily life.
2. The second is, it depends directly on the radius of the pipe, how? Think that what would happen if radius increases, if radius increases then its cross-sectional area also increases, if its cross-sectional area increases then the fluid gets more space to travel and suffer a little friction if friction is small then the flow rate increases automatically.
3. It is also a daily basis phenomenon, if any road is narrow then it suffers high traffic, but a broader road is free from traffic. The same is here. And the third is flow rate is inversely proportional to the viscosity, with larger viscosity larger friction then larger opposition, and then smaller velocity than a smaller flow rate.
4. And fourth, it is inversely proportional to the length of the pipe, how? If length increases then the time of friction to the wall also increases, and friction increases the same as above.

Poiseuille’s law statement

Poiseuille’s law statement: Poiseuille’s law is a principle in fluid dynamics that states that the flow rate of a fluid through a pipe or vessel is proportional to the pressure drop across the pipe and inversely proportional to the viscosity of the fluid and the length of the pipe. The law is named after the French physician Jean Léonard Marie Poiseuille.

Poiseuille’s law formula derivation

So, now we are going to derive a formula for the rate of flow of fluid volume per second.

Let’s take a cylinder of radius $R$ and length $L$ as shown below,
And flowing fluid of viscosity $\eta$, and $dr$ is the small distance between two cylindrical laminae. For an understanding see the diagram below.

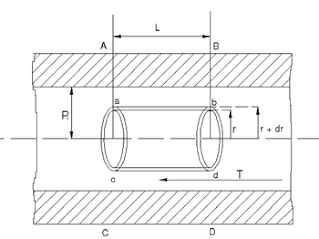
When a fluid is in the pipe then the force of viscosity generated due to the friction between the two lamina is given below:
$$F = -\eta A\left(\frac{dv}{dr}\right)$$
Where $A$ is the curved surface of the lamina with radius $r$ and length $L$ that is;
$$A = -2\pi rL$$
And $\frac{dv}{dr}$ is the velocity gradient, which means velocity changes with a change in radius.
Here sign is negative because this force opposes the velocity of the fluid.
Then put all the values F become-
$$F= -2\pi\eta rL\left(\frac{dv}{dr}\right)$$
And we know that fluid is flowing through the pipe due to pressure difference-
$$P = P_1-P_2$$
This pressure can be expressed in external force per unit area, then force is given as;
$$F = P\pi r^2$$
In equilibrium condition, the external force became equal to the laminar frictional force, viscous force. Equating both forces we get- Here we take only the magnitude
$$P\pi r^2 = 2\pi\eta rL\frac{dv}{dr}$$
After simplification, we get the-
$$\frac{dv}{dr} = \frac{Pr}{2\eta L}$$
Then,  $$ dv =\left(\frac{Pr}{2\eta L}\right)dr$$. Now integrating both sides from r to R, we get
$$\int dv = \frac{P}{2\eta L}\int_r^ R {rdr}$$
On solving we get-
$$v = \left[\frac{P}{4\eta L}\right]\left(R^2-r^2\right)$$

Now applying the equation of continuity, we get $V = A_1v_1=A_2v_2$, Where V is volume.

Then for a small cross-sectional area dA, we get a small volume of fluid that is dV
$$dV = dA\times v$$ Putting all values, we get-
$$dV = 2\pi rdr\times P\left(\frac{R^2-r^2}{4\eta L}\right)$$
On solving we get-
$$dV = \frac{P\pi\left(r.R^2-r^3\right)}{2\eta L}dr$$
Again integrating both sides from 0 to R because we want to find the whole volume of fluid in the pipe. Then we get-
$$\int{dV} = \frac{P\pi}{2\eta L}\int_0^ R\left[r.R^2-r^3\right]dr$$

On solving we get-
$$\begin{align*}V& = \frac{P\pi}{2\eta L}\left[\frac{\left(R^2.R^2\right)}{2}-\frac{R^4}{4}\right]\\
V&= \frac{P\pi}{2\eta L}\left[\frac{R^4}{2} – \frac{R^4}{4}\right]\end{align*}$$
On solving we get
$$V = \frac{P\pi R^4}{8\eta L}$$
This is the fluid that is flowing per second through the pipe. It is also denoted by $Q$. Watch this video for more reference.

Applications of poiseuille’s law

Poiseuille’s law has a number of applications in different fields, including:

1. Cardiology: The principle is used to predict blood flow in the cardiovascular system and to calculate blood pressure.
2. Chemical Engineering: It is used to design pipelines, storage tanks, and other fluid handling systems.
3. Petroleum Engineering: Poiseuille’s law is used to predict the flow of oil and gas through pipes.
4. Aerospace Engineering: The law is used to design fuel systems for aircraft.
5. Mechanical Engineering: It is used to design hydraulic systems for machinery and vehicles.
6. Environmental Engineering: Poiseuille’s law is used to predict the flow of water and other fluids in natural systems such as rivers, lakes, and groundwater systems.
7. Medical Equipment Design: The principle is used in the design of medical equipment such as intravenous pumps, dialysis machines, and blood pressure monitors.
8. Microfluidics: Poiseuille’s law is used to predict the flow of fluid in microfluidic systems, which are used in various applications, including drug delivery, biosensors, and lab-on-a-chip devices.

Frequently Asked Questions – FAQs

Stay tuned with Laws Of Nature for more useful and interesting content.