So today, we are going to talk about the concept of Torricelli law and the speed of EFFLUX and we will also derive the expression for the speed of efflux. This concept is the application of the Bernoulli principle. This is a very interesting phenomenon of hydrodynamics, this law is given by Italian scientist  Evangelista Torricelli in 1643. He calculates the velocity of fluid which are flowing as a jet from a hole in a tank.

Going further in the article, we have to understand the meaning of efflux first.
Then, what is efflux? If we talk about the efflux then efflux is nothing,  but it is a simple flowing of fluid just like a jet from a very tiny hole ie. Orifice, and it is necessary that the cross-sectional area of the orifice is very small as compared to the cross-sectional area of the tank.[latexpage]

Many of us must have seen, the flowing of fluid through a hole of a tank like a jet, and we have seen that this flowing fluid falls to the ground at some distance from the base o the tank. This distance from the base of the tank is called the range of fluid jet.
Now we are going to talk about the Torricelli law.

TORRICELLI LAW

If we talk about the Torricelli law then Torricelli law only tells us about the speed of efflux. And says that if a tank is filled with the fluid to the height h, above the orifice, then the speed of efflux is equal to the speed of free fall of a drop of fluid from the free surface of the fluid to the orifice.
This velocity of efflux can be found by equating the kinetic energy gained to the potential energy lost during the free fall of a drop of fluid. Now we are going to derive the formula for the speed of efflux.

DERIVATION

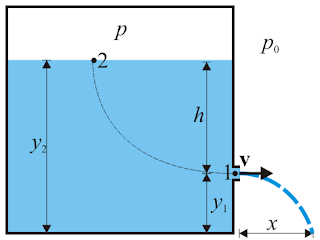
Let’s take a tank, in which fluid is filled to the height Y and the height of the orifice from the base of the tank is y.
Then the height of the fluid above the orifice is h = Y – y
And the elements at the free surface of the fluid of the tank are, $A_2, v_2, p_2$, and at the orifice is, $A_1, v_1, p_1$, and ρ is the density of the fluid.
If the tank is open at the top then p2 = p(atm) and p1 = p(atm) because the orifice is always open to the atmosphere.

Then applying equation of continuity , we get;
\begin{align*}
A_1v_1& = A_2v_2\\
v_2 &= \frac{A_1v_1}{A_2}
\end{align*}
Here $A_1v_1$ is small because the orifice is very small, and $A_2$ is large then on solving we get $v_2$ is very very small and seems negligible, so we take $v_2$  as zero.

Now applying the concept of Bernoulli principle
$$
p_1 + \rho gy + \frac{1}{2}\rho v_1^2 = p_2 + \rho gY$$
Here $\displaystyle{\frac{1}{2}\rho v_2^2}$ is zero because $v_2$ seems us zero.
So then-
$$
\frac{1}{2}\rho v_1^2 = (p_2 – p_1) + \rho g(Y -y)$$
And we know that, $Y – y = h$
So, it becomes-
\begin{align*}
\frac{1}{2}\rho v_1^2& = (p_2 -p_1) + \rho gh\\
v_1^2&= 2gh + \frac{2(p_2 – p_1)}{\rho}
\end{align*}
Then velocity of efflux is-
$$
v_1 = \sqrt{2gh + \frac{2(p2 – p1)}{\rho}}\qquad (p_1 = p(\text{atm})
$$
This formula is applicable when the tank is closed.
If tank is open then $p_2$ became p(atm).
And formula became-
$$
v_1 = \sqrt{2gh}$$   [p_2-p_1 = 0], because both are atmospheric pressure.
In kinematics, this formula is the velocity of free-falling objects.

RANGE OF FLUID JET

If the fluid is flowing like a jet then it must be some horizontal distance, that is called range.
Then this range can be simply calculated by multiplying the velocity of efflux and time taken by it to striking the ground. If y is the height of the orifice and Y is the height of the fluid column, Then the time taken by it to coming the ground is given as-
Applying the second equation of motion, we get-
\begin{align*}
y& = ut + \frac{1}{2}gt^2\\
y& = \frac{1}{2}gt^2\qquad [ ut = 0]\\
\text{Then}\; t& = \sqrt{\frac{2y}{g}}
\end{align*}
Then the range is-
\begin{align*}
R& = v_1\times t = \sqrt{2gh}\times \sqrt{\frac{y}{g}}\\
R& = \sqrt{4yh} = 2\sqrt{yh}
\end{align*}
Then maximum range is given as follows:
$$R = 2\sqrt{yh} = 2\sqrt{y(Y – y)}$$
Differentiate Range w.r.t to y, we get-
$$R'(y) = 2 \left[\frac{1}{{2\sqrt{y(Y – y)}}} \times(Y-2y)\right]$$
Equating R'(y) equal to 0
$$\frac{(Y -2y)}{\sqrt{y(Y-y)}} = 0$$
We get $Y – 2y =0$
Then double differentiation of Y-2y w.r.t to y, then we get (-2) which is less than 0, so it is Maxima. Coordinates $\displaystyle{y = \frac{Y}{2}}$ is point of Maxima
Putting value of $\displaystyle{y = \frac{Y}{2}}$ in the formula of range, then we get-
\begin{align*}
R& = 2\sqrt{\frac{Y\left[Y -\left(\frac{Y}{2}\right)\right]}{2}}\\
R& = 2\sqrt{\frac{Y^2}{4}} = Y
\end{align*}
It means its maximum range is equal to the height of the fluid column in the tank. Watch this video for more reference.