Time period of oscillation of bar magnet in a uniform magnetic field derivation

In this article, we are going to derive an expression for the time period of oscillation of a bar magnet in a uniform magnetic field, so without wasting time, let’s get started…

Derivation for the time period of oscillation of a bar magnet

What is a magnetic dipole?

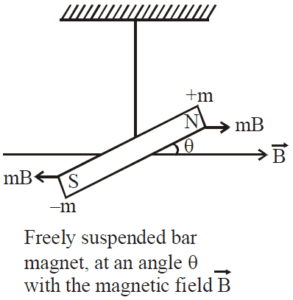
A magnetic dipole is the arrangement of two equal and opposite magnetic poles separated by a small distance of $2l$. It is described by the magnetic dipole moment $(\vec{M})$.

What is a magnetic dipole moment?

The magnetic dipole moment of a magnetic dipole is defined as the product of the magnetic pole strength and the magnetic length. It is a vector quantity directed from S-pole to N-pole. $$\vec{M}=\vec{m}\times 2\vec{l}$$ where $m$ is the magnetic pole strength and $2l$ is the length between their magnetic poles.

Torque, and relationship with the time period

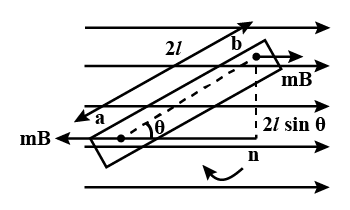
When a magnetic dipole (bar magnet) is placed in a uniform magnetic field, then it experiences a torque. This torque is given by the product of the force applied and the perpendicular distance between the forces. The value of Torque can be given as $$\tau = 2l\sin\theta \times \vec{F}$$ Now, the force applied on each magnetic pole can be given as the product of the pole strength and magnetic field. $$\vec{F}= mB$$

Suggested Reading:

• Torque on the magnetic dipole (bar magnet) in a uniform magnetic field, class 12

Now substitute the value of force $\vec{F}$ to the above formula of torque. After substitution we get: $$\tau=(mB)\times 2l\sin\theta$$ It can be rewritten as follows: $$\tau=(m\times 2l)B\sin\theta$$ We know that $(m\times 2l)$ is nothing but the expression of magnetic dipole moment, and we can say simply write $(M)$ in place of this expression. Now, new expression of torque can be given as: $$\tau =MB\sin\theta$$ In vector form, it can be given as: $$\tau =\vec{M}\times \vec{B}$$ Which is cross product of magnetic moment $(\vec{M})$ and magnetic field $(\vec{B})$. Now, since the magnetic dipole experiences a torque, then it can also experience angular acceleration as the value of θ keeps changing. This is due to the moment of inertia of the magnetic dipole and hence it keeps oscillating. Considering these factors, the equation of torque can be given as $$\tau =I\alpha$$ where $I$ is the moment of inertia of the dipole and $\alpha$ is the angular acceleration of the dipole. Now we can combine both the equations of torque and we get: $$I\alpha =MB\sin\theta$$ For small angular displacement $\theta$, we get: $$I\alpha = MB\theta$$ $$\implies \quad \alpha =\frac{MB}{I}\theta$$ Since the magnetic dipole undergoes oscillations which are the type of angular simple harmonic motion. We can compare the equations of simple harmonic motion with $\alpha$. On comparing, we see that: $$\alpha =\omega^2\theta$$ Putting value of $\alpha$ in above equation, we get: $$\omega^2\theta =\frac{MB}{I}\theta$$ or $$\omega^2 =\frac{MB}{I}$$ Where $\omega$ is the angular frequency. And in simple harmonic motion, the time period of the oscillations is given by the formula: $$T=\frac{2\pi}{\omega}$$ Therefore, on substituting the value of $\omega$, we get the time period of the dipole as follows: $$T=2\pi\sqrt{\frac{I}{MB}}$$ From this equation, expression of the magnetic field can be given in the terms of the time period as follows: $$B=\frac{4\pi^{2}I}{MT^2}$$

Stay tuned with Laws Of Nature for more useful and interesting content.