In this short piece of article, we will discuss the oscillation of a freely suspended bar magnet in a uniform magnetic field. We also show that this oscillation is a simple harmonic in nature and will also derive an expression for the time period of oscillation of a freely suspended bar magnet, so let’s get started…
Oscillation of a freely suspended magnet
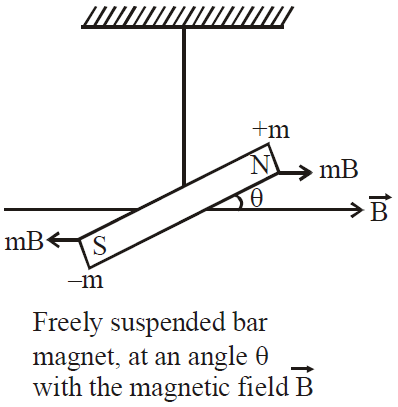
Let’s take a bar magnet and place it into a uniform magnetic field. As we know that in the equilibrium position, the magnetic dipole lies along $\vec{B}$. When it is slightly rotated from its equilibrium position and released, it begins to vibrate about the field direction under the restoring torque, given as $$\tau=-mB\sin\theta$$ Here negative sign indicates that the direction of torque $\tau$ is so as to decrease $\theta$.
For the small angular displacement $\theta$, $\sin\theta =\theta$. $$\therefore\quad \tau =-mB\theta$$
If $I$ is the moment of inertia of the magnetic material, then the deflecting torque on the magnetic is $$\tau =I\alpha = I\frac{d^2\theta}{dt^2}$$ In the equilibrium condition, $$\text{Deflecting torque = Restoring torque}$$ $$\therefore\quad I\frac{d^2\theta}{dt^2}=-mB\theta$$ $$ \text{or}\qquad \frac{d^2\theta}{dt^2}=-\frac{mB}{I}\theta=-\omega^2\theta$$
Here, you can clearly see that the angular acceleration $\frac{d^2\theta}{dt^2}$ is directly proportional to angular displacement $\theta$. Hence the oscillation of a freely suspended magnet in a uniform magnetic field is simple harmonic. The time period of oscillation of a freely suspended magnet in a uniform magnetic field is given by using the above relation as $$\boxed{T=\frac{2\pi}{\omega}=2\pi\sqrt{\frac{I}{mB}}}$$
Read Also
- The time period of oscillation of bar magnet in a uniform magnetic field derivation
- Torque on the magnetic dipole (bar magnet) in a uniform magnetic field, class 12
Stay tuned with Laws Of Nature for more useful and interesting content.