In this article, we will discuss the tangent galvanometer – principle, construction, theory, and its working, so let’s get started…
What is tangent galvanometer?
Tangent Galvanometer – Tangent galvanometer is a device which is used to measure very small currents. It is a type of moving magnet galvanometer, and working is based on tangent law.
A tangent galvanometer is one of the first measuring instruments used to measure electric current. It works by using a compass needle to compare a magnetic field generated by the unknown current with the Earth’s magnetic field. It was first described by Johan Jakob Nervander in 1834.

Principle of tangent galvanometer
A tangent galvanometer works on the principle of tangent law.
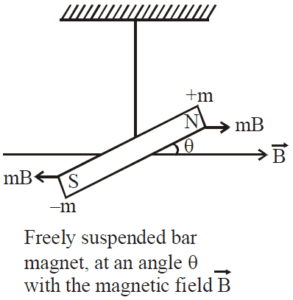
The magnetic needle of the galvanometer is subjected to the two perpendicular magnetic fields. One of these two perpendicular magnetic fields is due to the horizontal components of the earth’s magnetic field, and the other is due to the passing of the electric current through the coil of the tangent galvanometer.
Under the influence of these two magnetic fields, the needle comes to rest and makes angle $\theta$ with $B_H$, such that $B=B_H\tan\theta$
Construction of tangent galvanometer
It consists of a circular frame of non-magnetic material mounted on the horizontal turntable. Three coils having 2, 50, 500 turns of insulated copper wire are wound on it. The ends of the coils are connected to the three base terminals.
A compass of non-magnetic materials is mounted in the center of the circular frame. It has a small center-pivot magnetic needle with a long, thin aluminum needle attached perpendicular to it.
Both are free to move on a horizontal circular scale graduated in degrees and divided into four quadrants of 0° – 90° each. A flat mirror is positioned at the base under the pointer. This removes errors due to parallax when reading pointer positioning.
Adjustment
- All nearby magnets and any other magnetic materials are removed away from the device.
- The tangent galvanometer is leveled with the help of leveling screws and the coil is so rotated that its plane becomes parallel to the length of the magnetic needle.
- In this position, the plane of the coil lies along the magnetic meridian.
- The compass box is rotated so that the pointer comes along the 0° – 0° line.
Theory and working of tangent galvanometer
The working of the tangent galvanometer is based on the tangent law. When no current is flowing through the coil, the magnetic needle is only influenced by the horizontal component of the earth’s magnetic field $B_H$. When a current $I$ flows through the coil then it creates a magnetic field $B$ along the axis of the coil perpendicular to the $B_H$.
Now the magnetic needle is influenced by the two perpendicular magnetic fields, and hence the magnetic needle comes to rest at an angle $\theta$ with $B_H$ such that $B=B_H\tan\theta$. This relationship is called tangent law.
Now the magnetic field at the center of the coil is $$B=\frac{\mu_0 NI}{2R}$$ Where $N$ and $R$ are the numbers of turns and radius of the coil. $$\therefore\quad \frac{\mu_0 NI}{2R}=B_H\tan\theta$$ $$I=\frac{2R B_H\tan\theta}{\mu_0 N}=K\tan\theta$$ Where $K=\frac{2R B_H}{\mu_0 N}$ is a constant of the tangent galvanometer called reduction factor. $$\therefore \quad I\propto\tan\theta$$ Thus, in the tangent galvanometer current is directly proportional to the tangent of the angle of deflection of the needle. Due to this characteristic, the galvanometer is known as a tangent galvanometer. Knowing the value of $K$ and $\theta$ we can find the value of the current flowing through the coil.
Read Also
Sensitivity of the tangent galvanometer
The sensitivity of the tangent galvanometer is defined as the ratio of change in deflection of the needle to the current producing that deflection. $$\text{Sensitivity}=\frac{d\theta}{dI}$$ A galvanometer is said to be sensitive if it gives large deflection for small current.
$$
\mathrm{I}=\mathrm{k} \tan \theta
$$
Differentiating both sides w.r.t. $\theta$
$$
\begin{aligned}
&\frac{\mathrm{dI}}{\mathrm{d} \theta}=\mathrm{k} \sec ^{2} \theta \\
&\therefore \frac{\mathrm{d} \theta}{d I}=\frac{1}{\mathrm{k} \sec ^{2} \theta} \\
&\therefore \frac{\mathrm{d} \theta}{d I}=\frac{\cos ^{2} \theta}{\mathrm{k}} \\
&\text{but}\; \mathrm{k}=\left(\frac{2 \mathrm{R} \mathrm{B_H}}{\mu_0 \mathrm{n}}\right) \\ &\therefore \frac{\mathrm{d} \theta}{d I}=\frac{\cos ^{2} \theta}{\left(\frac{2 \mathrm{R} \mathrm{B_H}}{\mu_0 n}\right)} \\
&\therefore \frac{\mathrm{d} \theta}{d I}=\frac{\mu_0 \mathrm{n} \cos ^{2} \theta}{2 \mathrm{R} \mathrm{B}_{\text {H }}}
\end{aligned}
$$
Thus the sensitivity of the tangent galvanometer can be increased by
- Increasing the number of turns of the coils
- Keeping the value of $\cos^2\theta$ small
- Decreasing the value of the earth’s horizontal magnetic field. It can be done by placing an auxiliary bar magnet below the magnetic needle such that it opposes the horizontal component $B_H$.
- Decreasing the value of $R$ of the coil.
Limitations in increasing sensitivity
- If the number of turns of the coil is increased then the radius of the coil will be not the same for all the turns. Radius will change because large numbers of turns lead to a thicker coil. But if the radius changes then the magnetic field at the center will also change.
- Increment in coil turns can increase the resistance of the coil of the tangent galvanometer.
- If the radius is made to be small then the magnetic field at the center will not be uniform.
- If $\theta$ decreases then accuracy will also decrease. Accuracy is maximum at $\theta = 45^{\circ}$.
Accuracy of the tangent galvanometer
Let $d\theta$ be a small error in measuring the deflection $\theta$ so that the corresponding error in measuring the current $I$ is $dI$, then
$$
\begin{array}
\quad \mathrm{I}=\mathrm{K} \tan \theta \ldots \ldots \ldots .(1) \\
\text { Differentiating both sides w.r.t. } \theta \\
\frac{\mathrm{dI}}{\mathrm{d} \theta}=\mathrm{K} \mathrm{sec}^{2} \theta \\
\therefore \quad \mathrm{dI}=\mathrm{K} \mathrm{sec}{ }^{2} \theta \cdot \mathrm{d} \theta \ldots \ldots .(2) \\
\text { Dividing equation (2) by (1) } \\
\therefore \frac{\mathrm{d} \mathrm{I}}{I}=\frac{k \cdot \sec ^{2} \theta \cdot \mathrm{d} \theta}{K \cdot \tan \theta} \frac{\mathrm{d} \theta}{\cos ^{2} \theta \cdot \frac{\sin \theta}{\cos \theta}} \\
\therefore \quad \frac{\mathrm{dI}}{I}=\frac{\mathrm{d} \theta}{\cos \theta \cdot \sin \theta}=\frac{2 \mathrm{~d} \theta}{2 \cos \theta \cdot \sin \theta} \\
\therefore \quad \frac{\mathrm{dI}}{I}=\frac{2 \mathrm{~d} \theta}{\sin 2 \theta}
\end{array}
$$
Now, here you can see that the accuracy is maximum when the error is minimum i.e the value of $dI/I$ is minimum. i.e the value of $\sin2\theta$ is maximum. See below: $$\begin{aligned} &\sin2\theta =1\\ &\therefore\; 2\theta = \sin^{-1}(1)\\ &2\theta =90^{\circ}\\&\therefore\;\theta =45^{\circ} \end{aligned}$$ Thus, the accuracy of tangent galvanometer is maximum at 45°.
| Condition of accuracy and sensitivity is contradictory to each other so they can not be combined in a single device. |
Stay tuned with Laws Of Nature for more useful and interesting content.