In this article, we are going to discuss what if a bar magnet as a magnetic dipole is placed in a uniform magnetic field, so let’s get find out…
Torque on the magnetic dipole in an uniform magnetic field
[latexpage]Let’s consider a bar magnet NS of length $2l$ placed in a uniform magnetic field $\vec{B}$. Let $q_{m}$ is the pole strength of each pole. Let the magnetic axis of the bar magnet makes an angle $\theta$ with a uniform magnetic field. See figure below:
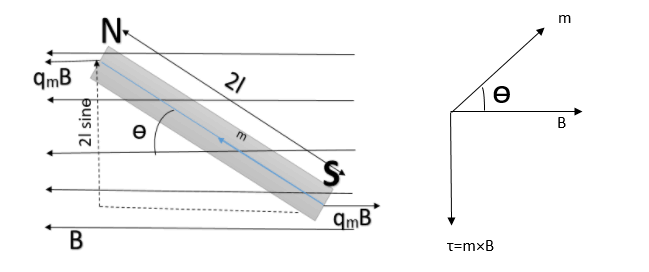
Force on North pole is $q_{m}B$, along $\vec{B}$, and force on South pole is $q_{m}B$ opposite to the $\vec{B}$.
We can see that the force on two pole is equal and opposite so they form a couple. The moment of couple or Torque is given as: $$\tau=\text{force}\times\text{perpendicular distance}$$ $$=q_{m}B\times 2l\sin\theta=(q_m\times 2l)B\sin\theta$$ or $$\boxed{\tau=mB\sin\theta}$$ where $m=q_m\times 2l$ is the magnetic dipole moment of the bar magnet. In vector notation, Torque can be given as: $$\vec{\tau}=\vec{m}\times \vec{B}$$
The direction of the torque $(\vec{\tau})$ can be given by the right-hand screw rule as indicated in the figure above (b).
Effects of the torque on the bar magnet
The effects of the torque $\vec{\tau}$ on the bar magnet is to align the magnet itself in parallel to the external magnetic field $\vec{B}$ So that’s why a freely suspended magnet aligns itself in the North-South direction because the earth has its own magnetic field that exerts a torque on the magnet tending to align in the earth’s field direction (North-South direction).
Special cases
1). When the magnet lies along the direction of the magnetic field.
θ = 0°, sin0° = 0, τ = 0
2). When the magnet lies perpendicular to the direction of the magnetic field.
θ = 90°, sin90° = 1, τ = mB
Thus, when θ is 90° (means magnet is perpendicular to the direction of the magnetic field) magnetic Torque is maximum. $$\tau_{max}= mB$$
Definition of the magnetic dipole moment
If the magnetic field (B) is of unit strength and θ is 90°, then $\tau = m$. So the magnetic dipole moment can be defined as the torque acting on the magnetic dipole placed perpendicular to the uniform magnetic field having unit magnetic field strength.
SI unit of magnetic moment
From $\tau =mB\sin\theta$, magnetic moment can be given as: $$m=\frac{\tau}{B\sin\theta}$$ Therefore, SI unit of magnetic moment is: $$\text{unit of m}=\frac{1 Nm}{1 T.1}=NmT^{-1}=JT^{-1}=Am^2$$
Watch this video for more reference:
Stay tuned with Laws Of Nature for more useful and interesting content.