In this article, we are going to derive an expression for the potential energy of a magnetic dipole in a uniform magnetic field. So let’s get started…
Derivation of the potential energy of a magnetic dipole in a uniform magnetic field class 12
Look at the following figure. [latexpage]
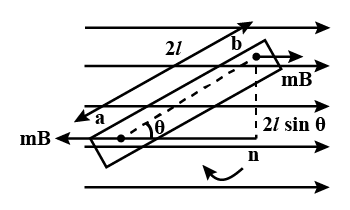
When a magnetic dipole is placed in a uniform magnetic field $(\vec{B})$ at angle $(\theta)$ with it, then it experiences a torque given as: $$\tau=mB\sin\theta$$ This torque tends the magnetic dipole to align with the direction of magnetic field $(\vec{B})$.
Suggested Reading:
- Torque on the magnetic dipole (bar magnet) in a uniform magnetic field, class 12
- Magnetic moment of atoms, electrons, nucleus, molecules, and elementary particles
This torque acts on the magnetic dipole in the direction of decreasing $\theta$. If the dipole is rotated against the action of this torque then some work has to be done. This work is stored as the potential energy of the dipole. The work done in turning the magnetic dipole through small-angle $(d\theta)$ is- $$dW=\tau{d\theta}=mB\sin\theta{d\theta}$$
If the dipole is rotated from initial position $\theta = \theta_1$ to final position $\theta =\theta_2$, then the total work done will be – $$W= \int{dW}=\int_{\theta_1}^{\theta_2} mB\sin\theta {d\theta}$$ $$ = mB[-\cos\theta]_{\theta_1}^{\theta_2}$$ $$=-mB(\cos{\theta_2}-\cos{\theta_1})$$
Suggested Reading:
- Magnetic dipole moment of a bar magnet
- what is bar magnet? definition, uses, properties, and types
- Magnetic dipole moment of a current-carrying loop, derivation class 12
This work done is stored as the potential energy $U$ of the dipole. $$\therefore\quad U=-mB(\cos{\theta_2}-\cos{\theta_1})$$ The potential energy of a dipole is zero when magnetic moment $(\vec{m})$ is perpendicular to the magnetic field $(\vec{B})$ i.e. $\vec{m}\perp \vec{B}$. So the potential energy of the dipole for any orientation $\theta$ can be obtained by putting $\theta_1 =90^{\circ}\; \text{and}\; \theta_2 = \theta$ in the above formula.
$$\therefore \quad U= -mB(\cos{\theta} -\cos{90^{\circ}})$$ or $$\boxed{U=-mB\cos{\theta}=-\vec{m}\cdot\vec{B}}$$
Special cases
- When $\theta=0^{\circ}$, $U=-mB\cos{0^{\circ}}=-mB$, Thus, the potential energy of a dipole is minimum when $\vec{m}$ is parallel to $\vec{B}$. In this state, magnetic dipole is said to be in stable equilibrium.
- When $\theta=90^{\circ}$, $U=-mB\cos{90^{\circ}}=0$
- When $\theta=180^{\circ}$, $U=-mB\cos{180^{\circ}}=+mB$, Thus, the potential enegry of a dipole is maximum when $\vec{m}$ is antiparallel to $\vec{B}$. In this state, the magnetic dipole is said to be in unstable equilibrium.
Stay tuned with Laws Of Nature for more useful and interesting content.