In the previous articles on the magnetic moment, we have discussed an expression for the magnetic moment that is $(\mu = IA)$. We have used this equation to obtain various forms of the magnetic moment. But this expression did not give a complete picture of the magnetic moment because this expression did not tell anything about the intrinsic magnetic moment of the material.
In this expression, we have ignored the intrinsic properties of their constituents particles. Without considering the intrinsic magnetism of the study of the elementary particles of magnetic moment is incomplete. So in this article, we are going to discuss the magnetic moment of various elementary particles by considering their intrinsic magnetic moment, so let’s get started…
How to calculate net magnetic moment?
When we talk about the magnetic moment of a system. Then it means we are talking about their net magnetic moment. Fundamentally, the contributions to any system’s magnetic moment come from two different sources. i.e
- Motion of the electric charge that is electric current, and second is.
- Intrinsic magnetism of elementary particles, such as the electron [latexpage]
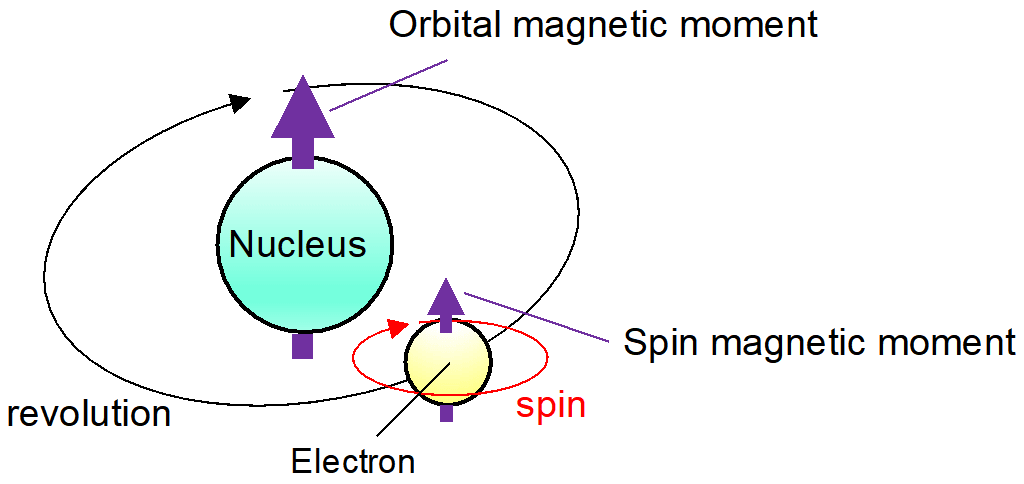
Contributions to the net magnetic moment due to the first source can be calculated from the knowledge of the distribution of all the electric currents inside the system. But on the other hand, the magnitude of each elementary particle’s intrinsic magnetic moment is a fixed number and can be measured experimentally to great precision. For example, the magnetic moment of an electron is measured to be $-9.284764\times10^{-24} J/T$.
The direction of the magnetic moment of any elementary particle is entirely determined by knowing the direction of its spin, here, the negative value to the electron’s magnetic moment indicates that the magnetic moment of an electron is antiparallel to its spin.
So the net magnetic moment of any system can be given as the vector sum of contributions including one or both types of sources. For example, the magnetic moment of a hydrogen-1 atom (the lightest hydrogen isotope, having a proton and an electron) is given as the vector sum of the following contributions:
- Intrinsic moment of the electron,
- Orbital motion of the electron around the proton,
- Intrinsic moment of the proton.
Similarly, the magnetic moment of a bar magnet can also be given as the sum of the contributing magnetic moments, including the intrinsic orbital magnetic moments of the unpaired electrons of the magnetic material and the nuclear magnetic moments.
Magnetic moment of an atom
To find the magnetic moment of an atom, individual electron spins are added to get a total spin, and individual orbital angular momenta are added to get a total orbital angular momentum, and then these two are added using the angular momentum coupling to get a total angular momentum. So for an atom having no nuclear magnetic moment, the magnitude of the atomic dipole moment is given as- $${\displaystyle {\mathfrak {m}}_{\text{atom}}=g_{\rm {J}}\,\mu _{\rm {B}}\,{\sqrt {j\,(j+1)\,}}}$$ where j is the total angular momentum quantum number, $g_J$ is the Landé g-factor, and $\mu_B$ is the Bohr magneton. The component of this magnetic moment which is along the direction of the magnetic field is given as- $${\displaystyle {\mathfrak {m}}_{{\text{atom}},z}=-m\,g_{\rm {J}}\,\mu _{\rm {B}}~}$$ Here negative sign occurs because electrons have negative charge. In the above equation, you can see there are two different m is used.
The integer m (not need to be confused with the magnetic moment, $({\displaystyle {\mathfrak {m}}})$ is called the magnetic quantum number or the equatorial quantum number, which can take any of (2j + 1) values. $${\displaystyle -j,\ -(j-1),\ \cdots ,\ -1,\ 0,\ +1,\ \cdots ,\ +(j-1),\ +j~}$$ Due to angular momentum, the kinetics of a magnetic dipole in a magnetic field is different from that of an electric dipole in an electric field. The field exerts a torque on the magnetic dipole which tends to align it with the field. However, the torque is proportional to the rate of change of angular momentum, so precession occurs.
| Precession: It is a slow movement of the axis of a spinning body around another axis due to a torque acting to change the direction of the first axis. |

This behavior is described by the Landau–Lifshitz–Gilbert equation given as follows: $${\displaystyle {\frac {1}{\gamma }}{\frac {{\rm {d}}\mathbf {m} }{{\rm {d}}t}}=\mathbf {m} \times \mathbf {H} _{\text{eff}}-{\frac {\lambda }{\gamma m}}\mathbf {m} \times {\frac {{\rm {d}}\mathbf {m} }{{\rm {d}}t}}}$$
In the above equation, γ is the gyromagnetic ratio, m is the magnetic moment, λ is the damping coefficient, and $H_{eff}$ is the effective magnetic field (the external field plus any self-induced fields). The first term describes the precession of the moment on the effective field, while the second is a damping term that relates to the dissipation of energy through interaction with the environment.
Magnetic moment of an electron
Electrons and many other elementary particles have also intrinsic magnetic moments. To explain this we need a quantum mechanical treatment that relates intrinsic magnetic moment to the intrinsic angular momentum of the particles as discussed in the article Electron magnetic moment. It is those intrinsic magnetic moments that give rise to the macroscopic effects of magnetism, and other phenomena, such as electron paramagnetic resonance. The magnetic moment of the electron is given as- $${\displaystyle \mathbf {m} _{\text{S}}=-{\frac {g_{\text{S}}\mu _{\text{B}}\mathbf {S} }{\hbar }},}$$ where $\mu_B$ is the Bohr magneton, S is electronic spin, and the $g_S$ is the g-factor whose value is 2 according to Dirac’s theory, but due to quantum electrodynamic effects it’s value is slightly bigger in reality: 2.00231930436. The deviation of the g-factor from 2 is known as the anomalous magnetic dipole moment of the electron.

Here, it should be noted that m is a negative constant multiplied by the spin, i.e. the magnetic moment of the electron is antiparallel to the spin, this can be understood with the following classic picture: If we imagine that the angular momentum of the spin is created by the mass of electrons rotating around an axis, the electric current that creates this rotation circulates in the opposite direction due to the negative charge of the electron; Such current loops create a magnetic moment that is antiparallel to the spin. But for a positron (the antiparticle of the electron) the magnetic moment is parallel to its spin.
Magnetic moment of the nucleus
The nucleus is a dense heavy complex part of an atom. The nuclear system comprises of the nucleons i.e protons and neutrons. The quantum mechanical properties of the nucleons are shown by their spin.
Since the electromagnetic moments of the nucleus depend on the spin of individual nucleons, these properties can be observed with measurements of the nuclear moments and, more precisely with the nuclear magnetic dipole moment. Most nuclei exist in their ground state, although nuclei of some isotopes have long-lasting excited states.
Every energy state of a nucleus of a given isotope is characterized by a well-defined magnetic dipole moment, the magnitude of which is a fixed number, which is often measured experimentally with great precision. Contributions from nucleons and measurement or prediction of their value can provide important information about the contents of the nuclear wave function nuclei along with the core map.
Magnetic moment of a molecule
The molecules have a well-defined magnitude of magnetic moment, which may depend on the molecule’s energy state. Usually, the overall magnetic moment of a molecule is the combination of the contributions given below in the order of their typical strength:
- Magnetic moments due to its unpaired electron spins (paramagnetic contribution)
- Orbital motion of its electrons, in the ground state which is often proportional to the external magnetic field (diamagnetic contribution).
- The combined magnetic moment of its nuclear spins, which depends on the nuclear spin configuration.
| Number of unpaired electrons | Spin-only moment (μB) |
| 1 | 1.73 |
| 2 | 2.83 |
| 3 | 3.87 |
| 4 | 4.90 |
| 5 | 5.92 |
Examples of molecular magnetism
Some examples of molecular magnetism are given below:
- The dioxygen molecule, O2, exhibits strong paramagnetism, due to unpaired spins of its outermost two electrons.
- The carbon dioxide molecule, CO2, mostly exhibits diamagnetism, a much weaker magnetic moment of the electron orbitals that is proportional to the external magnetic field.
- The nuclear magnetism of a magnetic isotope such as 13C or 17O will contribute to the molecule’s magnetic moment.
- The dihydrogen molecule, H2, in a weak (or zero) magnetic field exhibits nuclear magnetism, and can be in a para- or an ortho- nuclear spin configuration.
Magnetic moment of elementary particles
In atomic and nuclear physics, the Greek letter μ is used to show the magnitude of the magnetic dipole moment. it is often measured in Bohr magnetons or nuclear magnetons. It is associated with the intrinsic spin of the particle and $\ell$ or the orbital motion of the particle of a system. The values of the intrinsic magnetic moments of certain particles are given in the following table:
Intrinsic magnetic moments and spins of some elementary particles
| Name of the particle (symbol) | Magnetic dipole moment (10−27 J⋅T−1) | Spin quantum number (dimensionless) |
| electron (e−) | −9284.764 | 1/2 |
| proton (H+) | 14.106067 | 1/2 |
| neutron (n) | −9.66236 | 1/2 |
| muon (μ−) | −44.904478 | 1/2 |
| deuteron (2H+) | 4.3307346 | 1 |
| triton (3H+) | 15.046094 | 1/2 |
| helion (3He++) | −10.746174 | 1/2 |
| alpha particle (4He++) | 0 | 0 |
Magnetic moment calculator
Use this calculator to calculate the magnetic dipole moment of any elementary particles.
Stay tuned with Laws Of Nature for more useful and interesting content.