In this article, we will learn How to draw √2 on a number line. To understand this topic one should know irrational numbers and their properties. Let’s dig in…
What is √2?
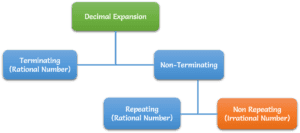
√2 is an irrational number. It is believed that it was discovered by the Greeks. Like all irrational numbers, its decimal expansion is also non-terminating and non-recurring. we can visualize the √2 as the length of the hypotenuse whose perpendicular and base are equal to one.
How to represent √2 on the number line?
First, we will understand the theory behind locating the √2 on a number line.
Theoretical part
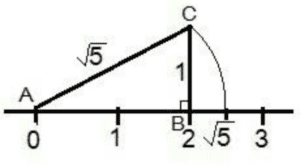
We can easily locate the √2 on the number line. with the help of the Pythagoras theorem we know that in a right-angle triangle the sum of the squares of perpendicular and base is equal to the square of the hypotenuse.
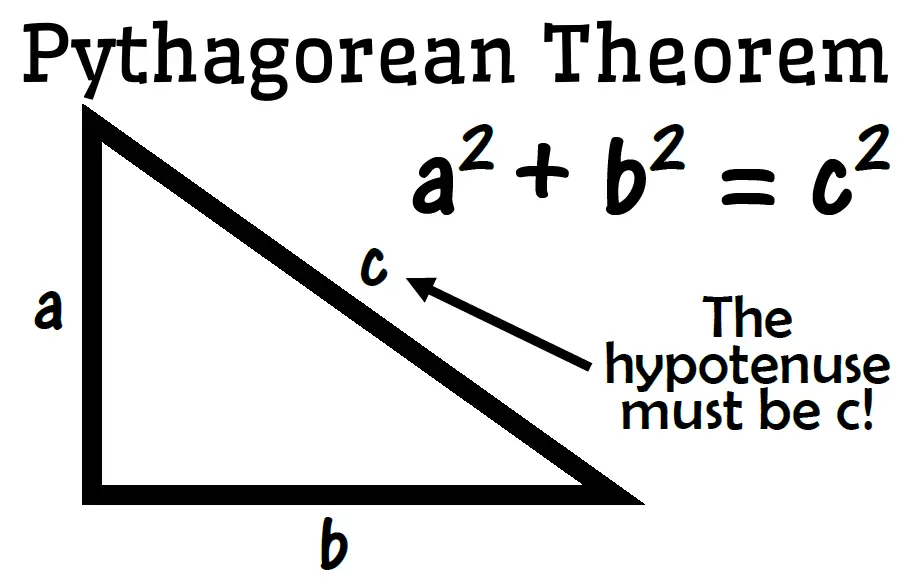
Hence a right angle triangle with base and perpendicular both equal to one will give a hypotenuse of length √2. $$\text{if B=1 , P=1, then}$$ $$H^2=P^2+B^2$$ $$H^2=1^2+1^2=2$$ $$H=\sqrt{2}$$
Construction method:
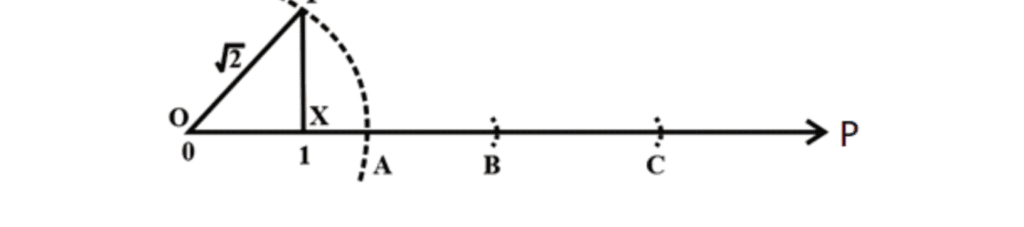
Step 1: Draw a number line.
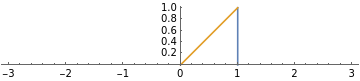
Step 2: Draw a line perpendicular line of 1 cm at 1 to this horizontal number line.

Step 3: Join the tip of the line with 0.
Step 4: Take a compass, place its tip on the 0 and the pencil on the tip of the perpendicular line, move the compass downwards, and mark the cut on a number line.
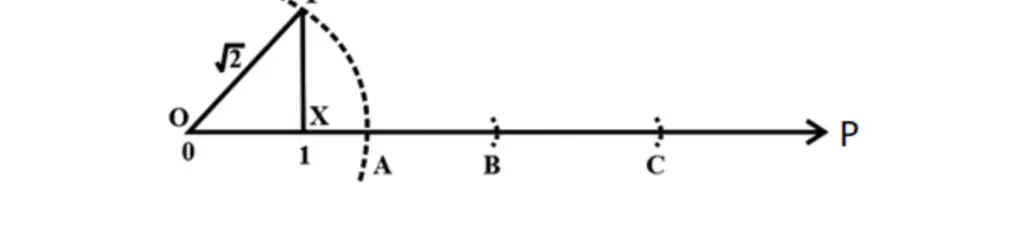
The distance from 0 to A is √2.
Conclusion
We can easily locate the √2 on a number line, with the help of a ruler, compass, and pencil. One should have the knowledge of Pythagoras’s theorem to understand the logic behind its construction. We hope the article helped you. Feel free to ask your doubts in the comment section.
Frequently Asked Questions – FAQs
What are the instruments we need to draw √2 on the number line?
Compass, ruler, and pencil
What is Pythagoras’s Theorem?
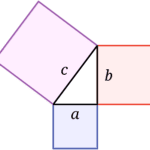
This theorem can be written as an equation relating the lengths of the legs a, b and the hypotenuse c, often called the Pythagorean equation:
Read Also
Stay tuned with Laws Of Nature for more useful and interesting content.