Introduction to Number system
This chapter discuss the various types of numbers in number system such as natural numbers, whole numbers, integers, rational numbers etc., we will cover these topics as per the level of a class 9th student.
Natural numbers
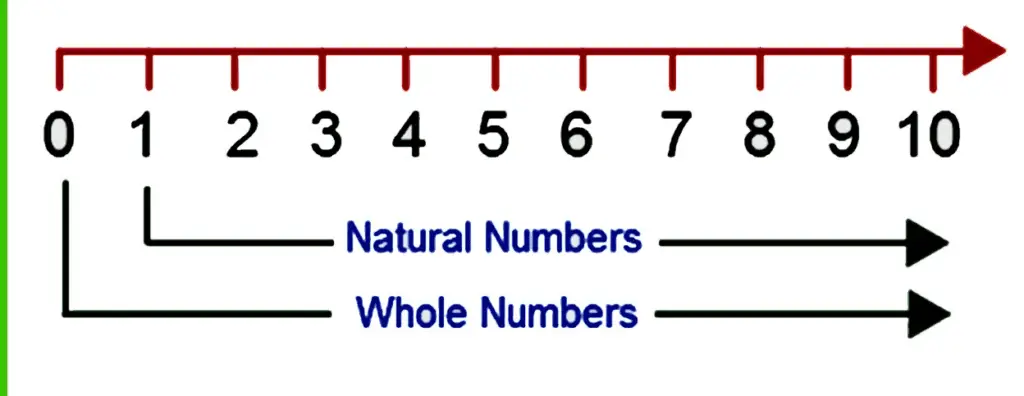
Natural numbers start from 1 and goes like 1,2,3,4… to infinity. They are also called positive integers. Natural numbers are denoted by symbol N.
For example 4,10,234 are natural numbers but 0,-1,-123 are not natural numbers.
Whole numbers
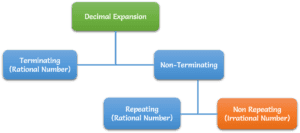
Whole numbers start from 0 and goes like 0,1,2,3… and so on till infinity. the concept of natural and whole can numbers is better understood by the figure given below. Whole numbers are denoted by symbol W.
Negative numbers

Integers
Integers is the combination of all negative integers, zero and positive integers. one should note that zero is neither a positive integer nor a negative integer. Integers are denoted by symbol Z.
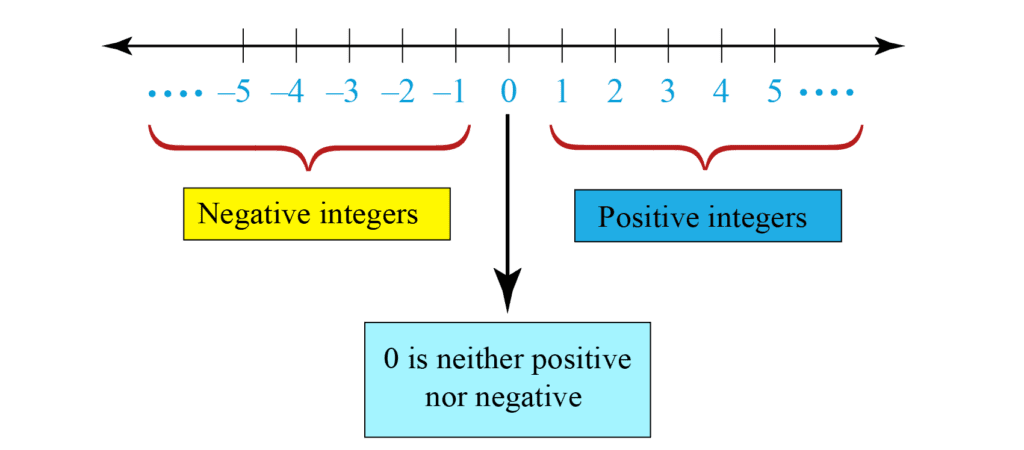
Rational numbers
A number ‘r’ is called a rational number, if it can be written in the form $$\frac{p}{q}$$ where p and q are integers and q ≠ 0.
For example 3 is a rational number since it can be written as $$\frac{3}{1}$$ similarly 4.5 can be written as $$\frac{45}{10} \: or \: \frac{9}{2}$$ we also note that $$\frac{45}{10} \: = \: \frac{9}{2}$$ and so we call them Equivalent rational numbers or fractions.
However, when we say that $$\frac{p}{q}$$ is a rational number we assume that p and q are co-prime integers i.e., p and q have no common factor other than 1.

Irrational numbers
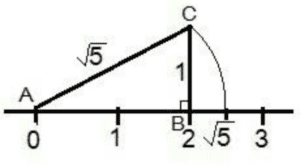
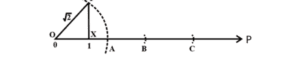
Irrational numbers are those numbers which can not be written in the $$\frac{p}{q}$$ form. Examples of Irrational number are $$\sqrt{2},\:\sqrt{3},\: \pi \:etc,$$.
Real numbers
Real numbers is the collection of all the rational and irrational numbers. This can be better illustrated by the figure given below
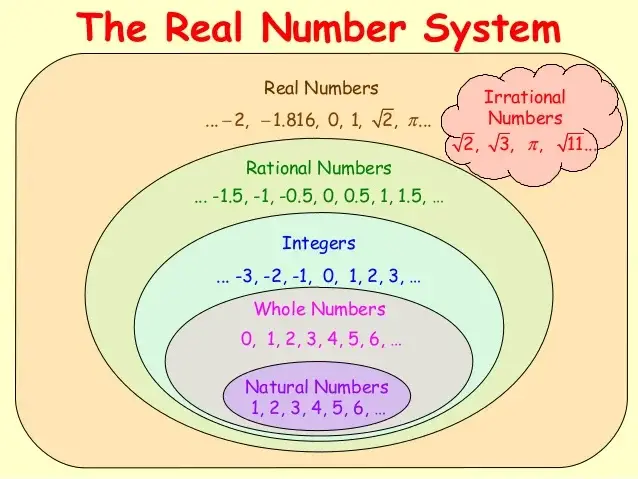
Test your concepts with our topic wise quiz
Summary
we can see that the basic numbers start from natural numbers and are extended to real numbers. A better understanding of this number system is very necessary. Feel free to ask your doubts in comment section.