In this article, we will study the Irrational numbers. Earlier we have discussed the rational numbers and their properties. Read this article to find out what irrational numbers are and their properties.
Irrational numbers
Definition: A number ‘s’ is called irrational, if it cannot be written in the form p/q, where p and q are integers, and q ≠ 0.

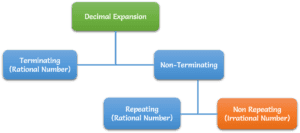
In other words, we can also say that all the numbers which are not rational numbers are called irrational numbers. Irrational numbers have a non-terminating and non-recurring decimal expression.
Examples of irrational numbers
Examples: √2, √3, √15, π, 0.10110111011110…, etc.,
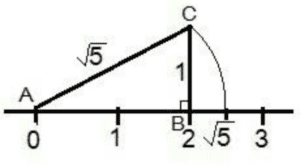
- √2 is an irrational number. √2 is a number whose square gives us the value 2, but we can not write it in the p/q form. Its decimal expression is also non-terminating and non-recurring. √2=1.41421356…
- π is also an irrational number. Its decimal expression is, π=3.141592653589793238462643…
- Any number whose decimal expression is non-terminating and non-recurring, for example, 1.01001000100001000001…, 2.0200200020002…, 3.040506070809010011…
- Given below is the list of some standard irrational numbers and their decimal expression
| Irrational number | value |
|---|---|
| π | 3.14159265…. |
| e | 2.7182818….. |
| √2 | 1.414213562… |
| √3 | 1.73205080… |
| √5 | 2.23606797…. |
| √7 | 2.64575131…. |
| √11 | 3.31662479… |
| √13 | 3.605551275… |
| -√3/2 | -0.866025…. |
| ∛47 | 3.60882608 |
Properties of rational numbers
Let us understand some basic properties of any irrational number.
- decimal expression of Irrational numbers is non-terminating and non-recurring.
- For any two irrational numbers, their LCM may or may not exist
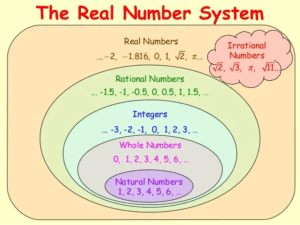
- These numbers are real numbers.
Closure property:
- Irrational numbers are not closed under addition
for example: √2 + (-√2)=0 - Irrational numbers are not closed under subtraction
for example: √2 -√2=0 - Irrational numbers are not closed under multiplication
for example: √2 *√2 = 2 - Irrational numbers are not closed under divison
for example: √2/√2 = 1
Associative property:
- Irrational numbers are associative under addition and multiplication.$$\sqrt{2}+(\sqrt{3}+\sqrt{5})=(\sqrt{2}+\sqrt{3} )+\sqrt{5}$$$$ \sqrt{2}*(\sqrt{3}*\sqrt{5})=(\sqrt{2}*\sqrt{3})*\sqrt{5}$$
Distributive property:
- Irrational numbers are distributive over multiplication. For example$$ \sqrt{2}*(\sqrt{3}+\sqrt{5})=\sqrt{2}*\sqrt{3}+\sqrt{2}*\sqrt{5}$$
Commutative Property:
- Irrational numbers are commutative under addition and multiplication. for example:$$\sqrt{2}+\sqrt{3}=\sqrt{3}+\sqrt{2}$$$$\sqrt{2}*\sqrt{3}=\sqrt{3}*\sqrt{2}$$
Properties of rational and irrational numbers:
- The Sum of any rational and irrational number is always an irrational number.
- Multiplication of any irrational and a non-zero rational number is always an irrational number.
- The difference between any rational and irrational number is an irrational number.
- The division of any non-zero rational and irrational number is an irrational number.
Conclusion
A number that can not be written in p/q form is called an irrational number. rational numbers and irrational numbers combine to form Real numbers. Irrational numbers do not hold any closure property like rational numbers.
Frequently Asked Questions – FAQs
Is 5 an irrational number?
No! it can be written in p/q form as 5/1. hence it is not an irrational number.
Are irrational numbers infinite?
Yes, there are infinite irrational numbers. But they are not in sequence and also do not follow any pattern.
Is √2 an irrational number?
Yes, √2 is an irrational number. The root of any number which is not a perfect square is an irrational number.
Does the decimal expression of irrational numbers terminate?
No! the decimal expression of any irrational number never ends or terminates, they also do not follow any repeating pattern in their decimal expression.
Interesting fact
π is one of the oldest found irrational number. For calculation purposes many scientist tried to find its value. Aryabhata found its value to a high degree of accuracy. Even nowadays the speed of a super computer is tested by measuring the value of π.