Here, we will learn the concept of Elasticity, the Reason for Elasticity. We will go in a basic meaningful manner to know about interatomic forces etc.

Material and its structure

Every material is made up of molecules which are in turn made up of atoms which are in turn made up of nucleus and electrons nucleus in turn being constituted by nucleons the nuclear forces operating between the nucleons are responsible for the structure of the nucleus.

The electromagnetic forces between the nucleus and electrons govern the structure of an atom, the interatomic forces govern the structure of a molecule, finally, the intermolecular forces govern the structure of the Materials.

But for neutral atoms and molecules how can there be any interatomic and intermolecular forces? Let’s find out :

Interatomic and intermolecular forces

As whole atoms and molecules are neutral and if we place them apart at a considerable distance they will feel no interatomic forces at all, but when the atoms are very close then due to the way of distribution of electrons in 3-D space around atoms despite they are overall neutral but can experience forces. This all is due to the way the distribution of electrons is always moving around atoms.

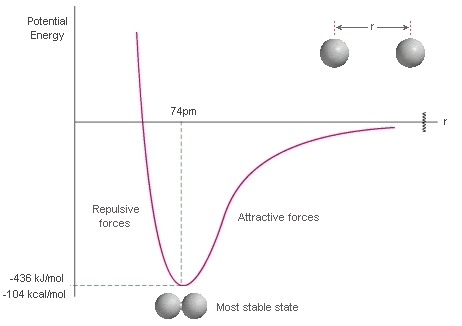
This variation of interatomic forces when atoms are at different distances is roughly approximated by the potential energy and interatomic distance curve ( U-r Curve ), Since Electrostatic force is conservative hence its Potential energy is defined and the curve is given by equation
[Latexpage]
\begin{align}
U = \frac{A}{r^12} – \frac{B}{r^6}
\end{align}

A typical U-r curve is shown

Force is obtain as the negative of slope of U-r curve because of equation

\begin{align}
F = -\frac{dU}{dr}
\end{align}

It’s known that the intermolecular forces also roughly behave the same as the interatomic forces behave.

It can be seen from the graph that around the lowest potential energy the slope of the graph is zero hence the net force is zero and the system is in equilibrium. And if we increase the interatomic distance the potential energy is negative it means that force is attractive  because
\begin{align*}
U = \frac{kq_{1}q_{2}}{r}
\end{align*}

From the above equation, we can see that if we have one positive and another negative charge the potential energy will be negative,

Hence the conclusion that when potential energy is negative force is attractive is made.

and also these charges will attract.

If we analyze the U-r Curve we know that this equilibrium is stable equilibrium if we change the distance between atoms they try to regain their positions of equilibrium. This is the core idea of elasticity.

Suggested reading: Equilibrium and analysis of U-r Curve.

Elasticity

In Physics we have an ideal concept of Rigid Bodies, bodies in which separation between the parties doesn’t change irrespective of the force applied to the system. But this is the ideal case and the real bodies don’t actually behave like it.

In real bodies, the separation between particles changes and They have a property known as elasticity, due to which they try to resist change in separation and tries to regain originality.

Definition of Elasticity

The tendency of a body to resist any change in its actual shape, size, and structure is Elasticity.

If the external forces which are trying to deform a body are removed then the body has the natural tendency to regain its original configuration. This tendency is elasticity. It’s because the particles are in stable equilibrium inside the material as all the forces balance each other.

Different types of bodies

his behavior of elasticity is shown till a limit of force after which the body is deformed and won’t be restored. As we can see with a rubber band.

Perfectly Elastic bodies are those which exactly regains the actual configuration.

Perfectly inelastic bodies are those which have no tendency to regain original configuration and once deformed they will remain deformed. Also known as inelastic or Plastic bodies.

Some bodies we deal with in real life regains configuration partially and gets partially deformed these are Partially Elastic Bodies.

Strain

It’s the fractional change in the configuration of a body due to external forces.
\begin{equation*}
Strain = \frac{change\hspace{2mm} in\hspace{2mm} config.}{actual\hspace{2mm}config.} = \frac{\Delta S}{S}
\end{equation*}

Note: By Default convention is that Any of the Strain should be reported positive . Hence if while correctly calculating if strain in obtained negative we have to report it positive.

also if somewhere we had given negative strain then the interpretation is that the finally the configuration of object is decreased hence change is negative.

There are three different types of strain defined:
1. longitudinal Strain
2. Shear Strain
3. Volumetric Strain

Longitudinal Strain

Let’s take a rod, initially, its length is “L”. The rod is pulled by equal and opposite forces. In this process the length of the rod is increased by $\displaystyle{\Delta L}$
the fractional change in length is known as Longitudinal Strain
\begin{align*}
Longitudinal\hspace{3mm} Strain = \frac{\Delta L}{L}
\end{align*}

When the length of the body increases then the longitudinal Strain is called as Tensile Strain.
When the body is compressed i.e the length is decreased the strain is known as Compressive Strain.

Note: it should be noted that the forces taken are equal and opposite because we don’t wanna to deal with the motion of body. As Net force equals zero the body remains in rest as it was initially.

Shearing Strain

Consider a body with a h square cross-section and suppose that it’s its base on contact with the floor is fixed. Also, suppose that a force is being applied on its top the force is tangential to the top surface. As shown here:

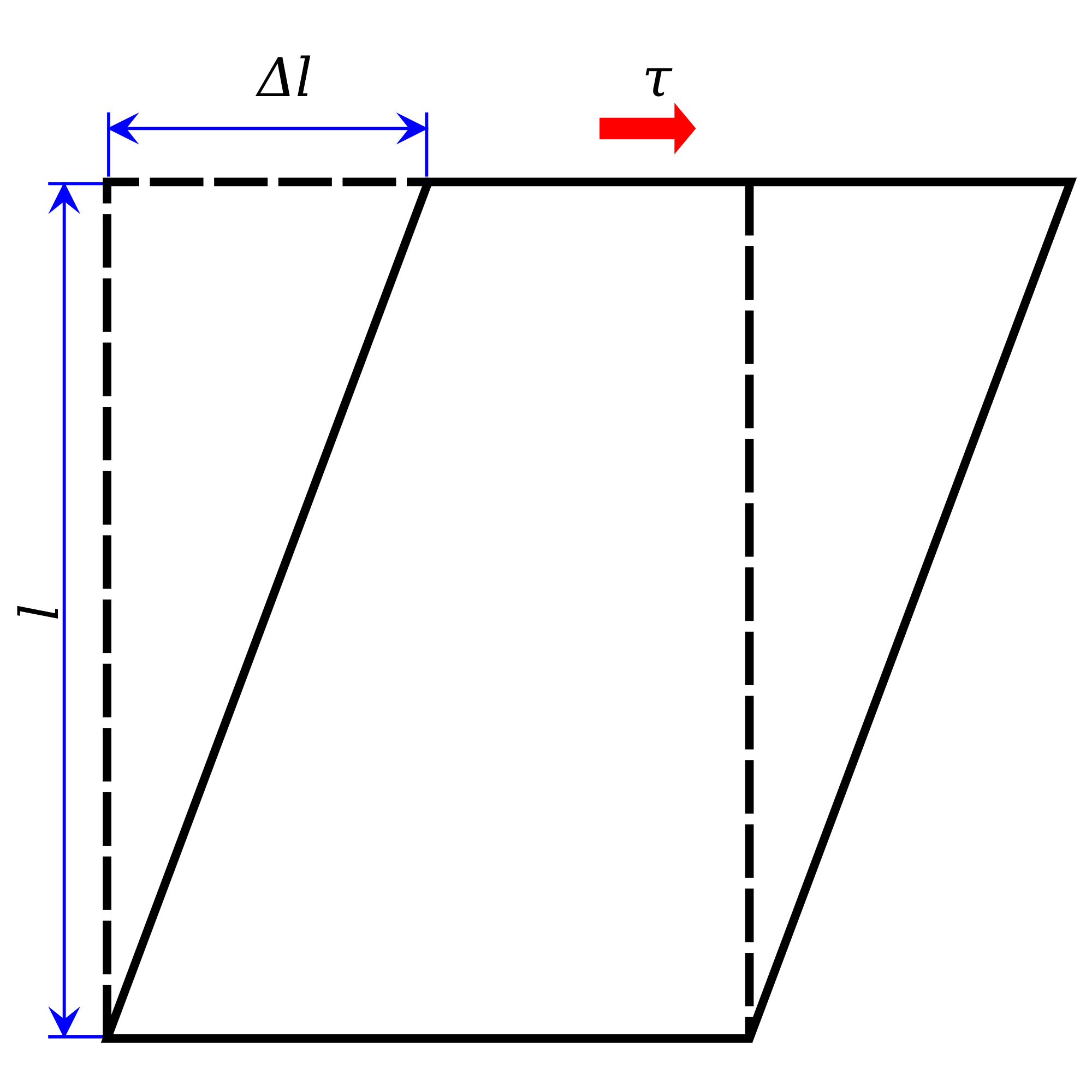
Using notations of above image. The shearing Strain is defined as
\begin{equation*}
Shear\hspace{3mm}Strain = \frac{\Delta L}{L} = \tan{\theta}
\end{equation*}
If theta is very small then we can use the approximation of
\begin{equation*}
\tan{\theta}= \theta \end{equation*}
$$
Where\hspace{2mm}\theta\hspace{2mm}is\hspace{2mm}in\hspace{2mm} radians. $$

Volumetric Strain

It’s the fractional change in volume of a body.
\begin{equation*}
= \frac{change\hspace{3mm}in\hspace{3mm} volume}{initial\hspace{3mm}volume}= \frac{\Delta V}{V}
\end{equation*}

Stress

Longitudinal Stress

Suppose a body is experienced by several forces such that the net force is zero, hence there will be no motion of the center of mass of the body, but the body can be deformed.

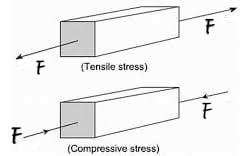
If the length of an object is increased the. It’s said to be tensile stress and if the length is decreased then the stress is said as Compressive stress.

If the body deforms it means that the separation between molecules/atoms changes hence internal Restoring forces appear also known as Restoring tension. Longitudinal Stress is defined as:
\begin{equation*}
= \frac{Restoring\hspace{2mm} tension}{Cross\hspace{2mm}section\hspace{2mm}area} = \frac{T}{A}
\end{equation*}

Note : longitudinal Stress also known as normal stress is defined for restoring force normal(perpendicular) to cross section for which we are writing it.

In general, when the body is in equilibrium all forces balance each other and the restoring tension equals the external force. Hence we often write longitudinal Stress as:
\begin{equation*}
= \frac{F}{A} \end{equation*}

Shear Stress

Shear Stress also known as tangential stress is defined as
\begin{equation*}
Shear \hspace{2mm}Stress = \frac{F_{t}}{A}
\end{equation*}

Here $\displaystyle{F_{t}}$ is tangential force to area which we consider.

Volumetric Stress

Suppose a body initially experiencing $\displaystyle{P_{1}}$ pressure and initially its volume is $\displaystyle{V_{1}}$ and now a pressure P is applied at every point and due to the pressure the volume of the body is reduced.

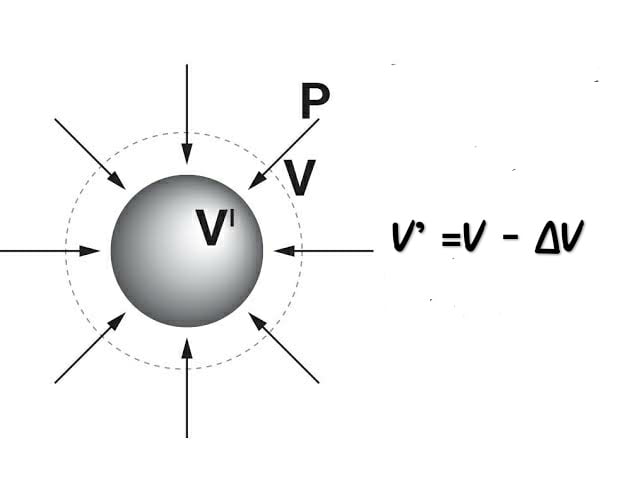
Volumetric stress is defined as the change in pressure
\begin{equation*}
Volumetric\hspace{2mm} Stress = \Delta P \end{equation*}

Additional Info

You might be thinking, whether stress scalar or vector? But the answer is it’s neither a scalar nor a vector. All three Stress defined here is Tensor quantities which you will learn in higher courses. but for calculation purposes in situations which we are given in high school, we can do calculations as we do with scalar Quantities.