Here we will learn the modulus of Elasticity, stress Strain Curve, and Hooke’s law of Elasticity. We know that when any force causes deformation to a body the body tries to regain its original configuration. The body which fully regains original configuration is perfectly Elastic and similarly partially Elastic, inelastic we defined.
Hooke’s Law
Let’s first think that, we are applying a force that’s causing deformation to a body and the body tries to regain its natural structure due to the property of Elasticity, Now what will happen if we increase the amount of force?
It’s observed that when we increase the force more than a limit then the body can’t even partially regain originality and will remain deformed. This Limit is Known as an Elastic Limit.
Hooke’s law states that Within the Elastic Limit Stress is directly proportional to Strain.
In physics Laws are deduced from experimental observations, hence Hooke’s law can be verified by various experiments.
Modulus of Elasticity
From Hooke’s law
[Latexpage]
\begin{equation*}
Stress \propto Strain
\end{equation*}
\begin{equation*}
\implies Stress = K\times Strain
\end{equation*}
Here The Proportionality constant is known as the Modulus of Elasticity.
Corresponding to each type of stress and strain. Three moduli of elasticity are defined.
Young’s Modulus of Elasticity
Defined for longitudinal Stress and longitudinal Strain
\begin{align*}
Longitudinal Stress \propto Longitudinal Strain
\end{align*}
\begin{equation}
\implies Y = \frac{ Longitudinal\hspace{2mm} Stress}{Longitudinal\hspace{2mm} Strain}
\end{equation}
Here the constant of Proportionality is known as Young’s Modulus of Elasticity and us denoted by “Y”.
Writing expression of longitudinal Stress and strain in equation (1) :
\begin{align*}
Y = \frac{T/A}{\Delta L/L}
\end{align*}
T is restoring tension.
Suggested: Learn Different types of Stress and Strain.
Shear Modulus ( Modulus of Rigidity )
Shear Stress is proportional to Shear strain within elastic limit, the proportionality constant is known as Shear Modulus of Elasticity also referred as Modulus of Rigidity. It is denoted by the Greek symbol $\displaystyle{\eta}$
\begin{align}
\eta = \frac{Shear\hspace{2mm} Stress}{Shear\hspace{2mm} Strain}
\end{align}
Bulk Modulus
It’s constant of Proportionality when volumetric stress is proportional to volumetric strain. It’s denoted by “B”
\begin{align}
B = \frac{Volumetric\hspace{2mm} Stress}{ Volumetric\hspace{2mm}Strain}\end{align}
If we write expressions of volumetric stress and strain equation (3) can be written as :
\begin{align}
B = \frac{dP}{dV/V}
\end{align}
Now if we analyze equation(4) we can see if dp is positive then dV should be negative and vice versa because if we increase pressure the volume will be decreased. Hence the whole term will always be -ve. But the convention is defined as that it should be reported +ve.
hence the Bulk Modulus is appropriately defined by putting a -ve sign in before as given below
\begin{align}
B = -\frac{dP}{dV/V}
\end{align}
Alternate expression for Bulk Modulus
$\displaystyle{\rho = density}$ and $\displaystyle{ V = volume}$
\begin{align}
\rho \times V = mass
\end{align}
Whether we compress or stretch a body we are changing intermolecular distances and the mass of the body remains constant.
Differentiating both sides of equation (6) w.r.t any parameter t.
\begin{align*}
\frac{d}{dt}(\rho V) = \frac{dm}{dt}
\end{align*}
$$
\implies \frac{d}{dt}(\rho V) = 0
$$
$$
\rho \frac{dV}{dt} + V\frac{d\rho}{dt} = 0
$$
$$
\rho \frac{dV}{dt} = – V\frac{d\rho}{dt}
$$
\begin{equation}
\implies \frac{dV}{V}= – \frac{d\rho}{\rho}
\end{equation}
Using equation (7) , equation (5) becomes
\begin{equation}
B = \frac{dP}{d\rho/\rho}
\end{equation}
This is an alternative expression for writing bulk modulus.
Similarly, we can do manipulation and can express Bulk Modulus for Gases, also for different thermodynamic processes we can express Bulk modulus with different expressions.
Compressibility
Compressibility is defined as the reciprocal of Bulk modulus. It’s denoted by K
\begin{equation}
K = \frac{1}{B} = – \frac{1}{V}\frac{dV}{dP}
\end{equation}
Poisson’s Ratio
Consider a cylindrical rod, if we stretch it then the length of the rod will increase and the radius/diameter decreases. The ratio of fractional change in radius to the fractional change in length is defined as Poisson’s Ratio. Denoted by $\displaystyle{\sigma}$
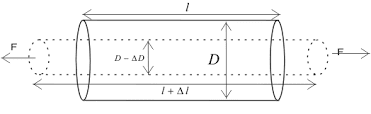
By convention, it is reported positive as stress and strain are reported positive hence a -ve sign is present to make the whole term positive.
\begin{align}
\sigma = – \frac{dR/R}{dl/l}
\end{align}
It’s a simple ratio and having no unit and dimensions.
Stress-Strain Curve
The Stress-Strain curves are obtained experimentally and are characteristic curves for each body.
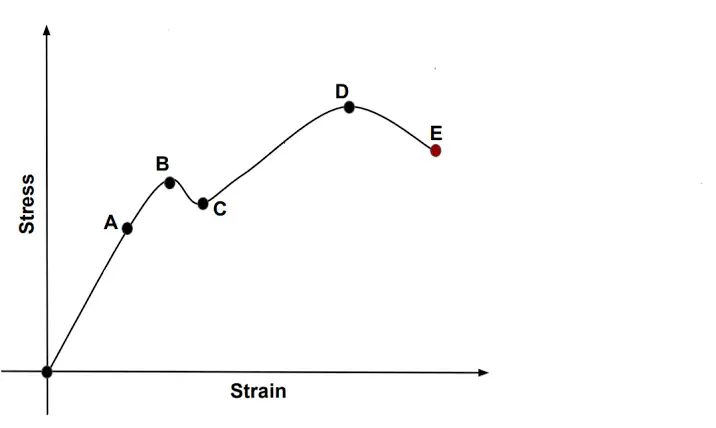
• From origin to A, Hooke’s law of Elasticity is valid and stress Strain is directly proportional. stress $\displaystyle{\propto}$ Strain.
• A to B Hooke’s law is not valid, for a small change in stress there is a larger change in strain, but still, the object is having a tendency to Fully regain, Point B is called Elastic Limit.
• After Elastic limit i.e point B, an object will not fully regain originality and will remain deformed. The region from B to E is known as Plastic Region.
• In regions C to D even if stress has decreased the strain will keep on increasing.
• Point D is the maximum stress the body can withstand and is known as breaking limit if more stress is applied the object will separate in parts
• Point E is the maximum strain the body can withstand it’s the maximum deformation the body can go. No more strain can be produced and is known as Fracture Limit.