In this article, we are going to derive an expression for the magnetic field due to a bar magnet at an arbitrary point around the bar magnet. So let’s get started…
Derivation for the magnetic field due to an bar magnet at an arbitrary point
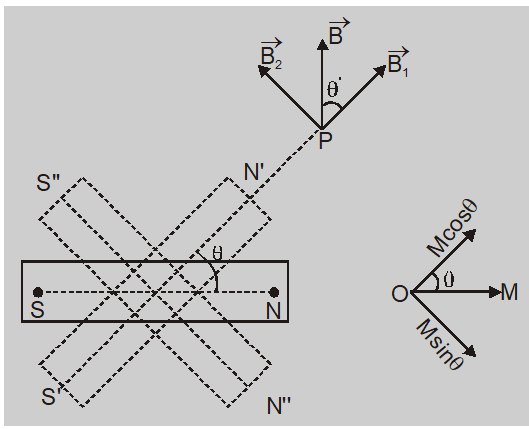
[latexpage] Let’s take a point P at a distance $r$ from the center of the bar magnet. Join the line from point P to the center of the magnet and let this line make an angle $\theta$ with the magnetic axis.
Magnetic field due to the bar magnet at an arbitrary point P has two magnetic field components i.e vertical components and horizontal components. Horizontal components of the magnetic field $\vec{B_1}$ is because if you see the above figure then you will find that the point P is on the axial line of a virtual magnet S’N’ having magnetic moment $2M\cos\theta$ and the vertical components of the magnetic field $\vec{B_2}$ is because if you again see the above figure then you will find that the point P is on the equatorial line of the virtual magnet S”N” with magnetic moment $M\sin\theta$.
Let $\vec{B_1}$ is the horizontal and $\vec{B_2}$ is the vertical components of the magnetic field. Then the expression of the magnetic field of both of the field components is:
$$\vec{B_1}=\frac{\mu_0}{4\pi}\cdot\frac{2M\cos\theta}{r^3}$$ $$\vec{B_2}=\frac{\mu_0}{4\pi}\cdot\frac{M\cos\theta}{r^3}$$
The total resultant magnetic field at point P is given as: $$\vec{B}=\sqrt{\vec{B_1}^2+\vec{B_2}^3}$$ Putting the values of $\vec{B_1}$ and $\vec{B_2}$ in above formula we get-
$$\vec{B_1}=\frac{\mu}{4\pi}\cdot\frac{M}{r^3}\sqrt{4\cos^2\theta+\sin^2\theta}$$ $$\vec{B_1}=\frac{\mu}{4\pi}\cdot\frac{M}{r^3}\sqrt{3\cos^2\theta+1}$$
From the above figure $\tan\theta^{\prime}$ is given by $\frac{B_2}{B_1}$ , so solving we get as below: \begin{equation*}\begin{split}\tan \theta^{\prime}&=\frac{B_{2}}{B_{1}}=\frac{\frac{\mu_{0}}{4 \pi} \frac{M \sin \theta}{r^{3}}}{\frac{\mu_{0}}{4 \pi} \frac{2 M \cos \theta}{r^{3}}}=\frac{1}{2} \tan \theta\\ \theta^{\prime}&=\tan ^{-1}\left(\frac{1}{2} \tan \theta\right)\end{split}\end{equation*}
Suggested reading:
- Derive an expression of the magnetic field at the axial point of a bar magnet class 12
- Define the term, magnetic field, uniform magnetic field, magnetic poles, magnetic axis, magnetic equator, and magnetic length with reference to a bar magnet
- Derive an expression of magnetic field at a point on the equatorial line of a bar magnet class 12
Stay tuned with Laws Of Nature for more useful and interesting content.