In this article, we will derive an expression for the magnetic field at a point on the axis of a bar magnet, so let’s get started…
Derivation of the magnetic field at the axial point of a bar magnet class 12
[latexpage]Let SN be a bar magnet of length $2l$ and magnetic pole strength of $q_m$. Suppose the point at which we wish to find the magnetic field, lies on the axis of the magnet at the distance $r$ from the center of the bar magnet. Here, P is the point where we want to find the magnetic field. See figure below:
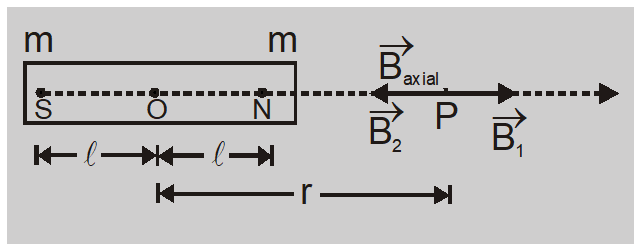
Let $B_1$ be the magnetic field experienced by the point P due to the North pole of the bar magnet and $B_2$ be the magnetic field experienced by the point P due to the South pole of the bar magnet. The net magnetic field $(B)$ experienced by the point P (lie on the axis of a bar magnet) is the algebraic sum of all the magnetic field acted on it, i.e $$B_{axial}=B_1 + B_2$$
So magnetic field due to the North pole of the bar magnet at the point P is: $$B_1=\frac{\mu_0}{4\pi}\cdot\frac{q_m}{(r-l)^2}\quad\text{along}\:\overrightarrow{NP}$$ And the magnetic field due to South pole of the bar magnet at the point P is given as: $$B_2=\frac{\mu_0}{4\pi}\cdot\frac{q_m}{(r+l)^2}\quad\text{along}\:\overrightarrow {PS}$$
So the net magnetic field at the point P is given as: $$B_{axial}=B_1 + (-B_2)$$
| In the above sum, $B_2$ is taken as negative because the direction of the magnetic field due to the south pole is opposite to the direction of the magnetic field due to the north pole of the bar magnet. |
Substitute the value of $B_1$ and $B_2$ in the above sum, we get-
$$B_{axial}=\left[\frac{\mu_0}{4\pi}\cdot\frac{q_m}{(r-l)^2}-\frac{\mu_0}{4\pi}\cdot\frac{q_m}{(r+l)^2}\right]$$ $$B_{axial}=\frac{\mu_0q_m}{4\pi}\left[\frac{1}{(r-l)^2}-\frac{1}{(r+l)^2}\right]$$ $$B_{axial}=\frac{\mu_0q_m}{4\pi}\left[\frac{4rl}{(r^2-l^2)^2}\right]$$
We know that $q_m\cdot 2l=M$, where M is the magnetic dipole moment of this magnetic dipole (bar magnet), so above equation can be rewritten as: $$B_{axial}=\frac{\mu_0}{4\pi}\cdot\frac{2Mr}{(r^2-l^2)^2}$$
For a short bar magnet, for which $(l<<<r)$ magnetic length (l) of the bar magnet is taken as negligible as compared to the distance (r) of the axial point P. So the reduced expression of magnetic field at the axial point of bar magnet is given as: $$B_{axial}=\frac{\mu_0}{4\pi}\cdot\frac{2M}{r^3}\quad\text{along}\:\overrightarrow {NP}$$
It is clearly visible that the direction of the magnetic field at the axial point due to a bar magnet is same as the direction of the magnetic dipole moment, i.e from S-pole to N-pole, so we can write: $$B_{axial}=\frac{\mu_0}{4\pi}\cdot\frac{2 \overrightarrow{M}}{r^3}$$
Stay tuned with Laws Of Nature for more useful and interesting content.