In this short piece of article, we will discuss magnetic permeability, relative permeability, magnetic susceptibility and relationship between magnetic permeability and magnetic susceptibility. So let’s get started…
What is Magnetic permeability?
Magnetic field is a component of electromagnetic waves. As we know that electromagnet waves can penetrate any material. But penetration does not happened at the same rate in all materials. It varies material to material because different material has different magnetic response when it is placed in external magnetising field.
In electromagnetism, permeability is the measure of the magnetization that a material receives in response to the application of a magnetic field. Permeability is usually represented by the Greek letter μ (italic). The term was coined by Oliver Heaviside in September 1885. [latexpage]
| The reciprocal value of the magnetic permeability is magnetic resistance. |
Definition of magnetic permeability
Magnetic permeability: It is the capability of the magnetizing field to penetrate any magnetic material. In other words, permeability is the measures of the extent to which a magnetic material is penetrated or permeated by the magnetic field.
Formula of magnetic permeability
The magnetic permeability of any magnetic material can be given as the ratio of magnetic induction $B$ to the magnetic intensity $H$. Mathematically, it is expressed as $$\mu=\frac{B}{B}$$
Unit of magnetic permeability
From the above equation, clearly we can see that SI unit of μ is $$\mu=\frac{\text{Tesla}}{ampere\cdot {meter}^{-1}}$$
| $\mu=tesla \cdot meter \cdot ampere^{-1}=Tm{A}^{-1}$ |
In SI units, permeability is measured in henry per meter (H/m) or equivalently in newton per square ampere $(N/A^{2})$. Therefore, dimensions of magnetic permeability is $[MLT^{-2}A^{-2}]$.
What is relative permeability?
Relative permeability is a dimension less quantity which is used to compare the permeability of substances to the other while considering the air or vaccum.
Relative permeability: It is the ratio of the permeability of the medium to the permeability of the free space. Mathematically, it is expressed as $$\mu_r =\frac{\mu}{\mu_0}$$
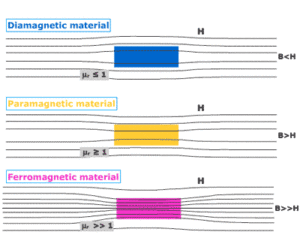
The relative permeability for vacuum is 1, i.e $\mu_r = 1$, for air, it is $\mu_r =1.0000004$, and for the iron, relative permeability may exceed to 1000.
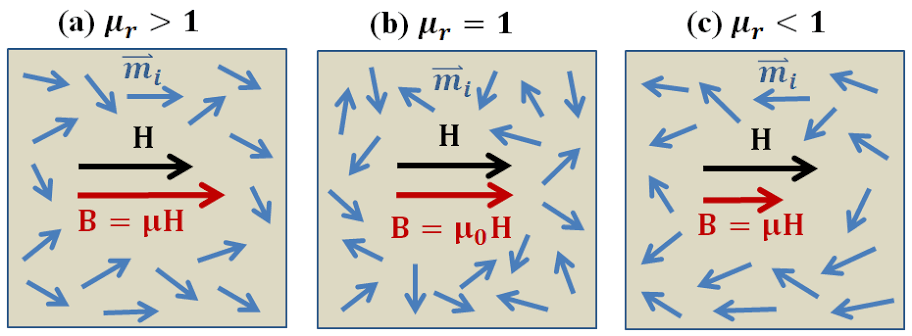
What is magnetic susceptibility?
We know that every magnetic material donot magnetize as the same way as other do. Because of their different atomic structure or electronic configuration. Due to this they have different ability to magnetize itself when they are placed in external magnetising field.
Magnetic susceptibility: It is the ability of the magnetic material to take up magnetization when it is placed in external magnetising field. It is defined as the ratio of the intensity of magnetization $M$ to the magnetising field intensity $H$. Mathematically, it is expressed as $$\chi_m =\frac{M}{H}$$
Magnetic susceptibility have the same quantity in its numerator and denominator, so it has no unit. Thus, it is dimensions less.
Suggested reading:
Relation between magnetic permeability and magnetic susceptibility
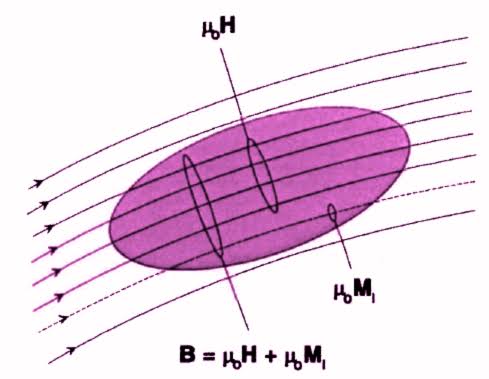
If a linear magnetic material, subjected to the action of a magnetising field intensity $H$, develops magnetisation $M$ and magnetic induction $B$; then $$\begin{aligned} B &=\mu_{0}(H+M) \\\text { But } B &=\mu H \\\therefore \quad \mu H &=\mu_{0}(H+M)\end{aligned}$$ $$\begin{aligned}\text { or } \mu&=\mu_{0}\left(1+\frac{M}{H}\right) \\ \mu&=\mu_{0}\left(1+\chi_{m}\right) \\\text { or } \mu_{0} \mu_{r}&=\mu_{0}\left(1+\chi_{m}\right)\\ \mu_{r}&=1+\chi_{m} \end{aligned}$$
Stay tuned with Laws Of Nature for more useful and interesting content.