In this article, we will derive an expression for the magnetic field due to the long straight current-carrying conductor using Ampere’s circuital law. So without talking more, let’s start…

AMPERE’S CIRCUITAL LAW: A SNAPSHOT

Let’s recall what Ampere’s circuital law states?

Ampere’s circuital law states that the line integral of magnetic field density (B) along an imaginary closed loop called amperian loop is equal to the product of current enclosed by the loop and permeability of the medium.

Mathematically, it is given as-[latexpage]
$$\oint{\mathbf{B}}\cdot{d{\mathbf{l}}}=\mu_0 I$$

Here, B and dl are going in dot product, since the direction of magnetic field (B) and dl is the same at each point on the loop.
Now, we will use this law to derive the magnetic field at a point due to an infinitely long straight current-carrying conductor.

DERIVATION FOR THE MAGNETIC FIELD DUE TO INFINITELY LONG STRAIGHT CURRENT-CARRYING CONDUCTOR

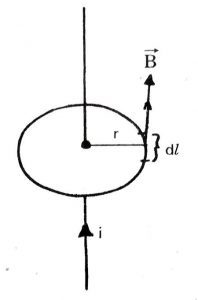
Let’s take an infinitely long straight current-carrying conductor. Mark a point P at the distance r perpendicular to the conductor. Make a circle around the wire taking r as a radius. This circular closed curve (circumference) is an imaginary closed line called the Amperian loop or path. Amperian loop can be different for different structures.

Let’s consider an infinitesimal length $d\mathbf{l}$ on the amperian loop at the same point. At every point on the amperian loop, the value of magnetic field (B) is constant because the perpendicular distance of that point from the axis of the conductor is fixed, another reason can be given to convey this assertion that the radius of the circle (amperian loop) will always be same, but its direction will be along the tangent on the loop at that point. See figure below:

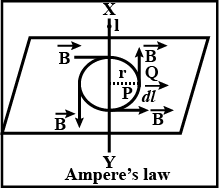
Now, according to the Ampere’s circuital law, the line integral of the magnetic field (B) around the closed curve C  (amperian loop) is equal the $\mu_0$ times the current enclosed by the surface. So from Ampere’s law, we get-

IN THE FORM OF MAGNETIC B-FIELD

\begin{align*} \oint_{C}\mathbf{B}\cdot d\mathbf{l}&=\mu_0 I\\ \mathbf{B}\oint_{C} d\mathbf{l}&=\mu_0 I\\ \mathbf{B}\cdot 2\pi r&=\mu_0 I\\ \mathbf{B}&=\frac{\mu_0 I}{2\pi r} \end{align*}

IN THE FORM OF MAGNETIC H-FIELD

\[\oint_{C}\mathbf{B}\cdot d\mathbf{l}=\mu_0 I\]
Divide both side by $\mu_0$, we get-
\begin{align*} \oint_{C} \frac{\mathbf{B}}{\mu_0}\cdot d\mathbf{l}&=I\\ \oint_{C} \mathbf{H}\cdot d\mathbf{l}&=I\\ \mathbf{H}\oint_{C} d\mathbf{l}&=I\\ \mathbf{H}\cdot 2\pi r&=I\\ \mathbf{H}&=\frac{I}{2\pi r} \end{align*}
Where H is magnetic field intensity in Ampere/meter (A/m).

IMPORTANT POINTS

Some important points related to this derivation is listed below:

• The magnetic field (B) at every point on the circle of radius r (amperian loop) is the same in magnitude.
• The magnetic field around the wire possesses cylindrical symmetry.
• The direction of the magnetic field at any point on the closed-loop or circle is tangential to it.
• The lines of the constant magnitude of the magnetic field form concentric circles. These circular lines are called magnetic field lines.
• Even if the wire is infinite length, the magnetic field due to it at a non-zero distance is not infinite.

Stay tuned with Laws Of Nature for more useful and interesting content.