This will be a short article, so without talking too much let’s get started…
Relation between induced charge and change in magnetic flux

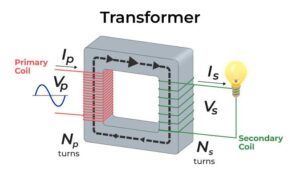
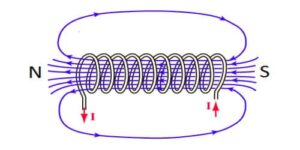
According to the faraday’s law, the induced EMF is given as $$ {\mathcal {E}}=\frac{\Delta \phi}{\Delta t}$$ If $R$ is the total resistance of the closed-loop, the induced current will be $$I=\frac{\mathcal {E}}{R} \quad or \quad \frac{\Delta q}{\Delta t} =\frac{\Delta \phi}{\Delta t}\cdot\frac{1}{R}$$ Hence, the charge induced in the loop in time $\Delta t$ is
| $$\Delta q =\frac{\Delta \phi}{R}= \frac{\text{Net change in magnetic flux}}{\text{Resistance}}$$ |
Clearly, we can see the induced current depends on the net change in magnetic flux and does not depend on the time interval $\Delta t$ of the flux change. Thus, the induced charge does not depend on the rate of change of magnetic flux.
Read Also
- Motional EMF, and energy consideration class 12
- Motional EMF from Lorentz force class 12
- Fleming’s right-hand rule (for generators)
- Motional EMF from Faraday’s law | definition, formula derivation
- Lenz’s law – statement, formula, application, and experiments
Stay tuned with Laws Of Nature for more useful and interesting content.