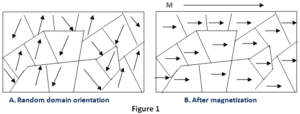
In this article, we are going to discuss the origin of paramagnetism class 12, so let’s get started… But Wait! Before discussing its origin, let’s discuss paramagnetism is brief first.
What is paramagnetism?
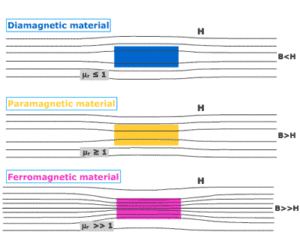
Paramagnetism Definition: Paramagnetism is a type of magnetism in which some specific materials are weakly attracted towards an externally applied magnetic field and form internally induced magnetic fields in the direction of the applied magnetic field.

Contrary to this behavior, diamagnetic materials are repelled by magnetic fields and induced magnetic fields in the opposite direction to the applied magnetic field. Most of the chemical elements and some compounds are materials that have paramagnetic properties.
They have a relative magnetic permeability slightly greater than 1 (i.e. a small positive magnetic susceptibility) and are therefore attracted towards magnetic fields. The magnetic moment induced by the applied field is linear in field strength and rather weak. [latexpage]
Typically, it requires a sensitive analytical balance to detect the effect, and modern measurements on paramagnetic materials are often performed with a SQUID magnetometer.
Origin of paramagnetism class 12
Origin of paramagnetism
Paramagnetism originates due to the presence of unpaired electrons in the materials. So most of the atoms with incompletely filled atomic orbitals are paramagnetic in nature, although there exists an exception such as copper.
Due to their spin, unpaired electrons have a magnetic dipole moment and act like small magnets. An externally applied magnetic field causes the electron’s spins to align parallel to the field, which causes a net attraction. Examples of some paramagnetic materials are aluminum, oxygen, titanium, iron oxide (FeO), etc. Therefore, a simple rule of thumb is used in chemistry to determine whether a particle (atom, ion, or molecule) is paramagnetic or diamagnetic.
- If all electrons in the particle are paired, then the materials made of this particle is diamagnetic.
- But if it has unpaired electrons, then the material is paramagnetic.
Magnetization retention
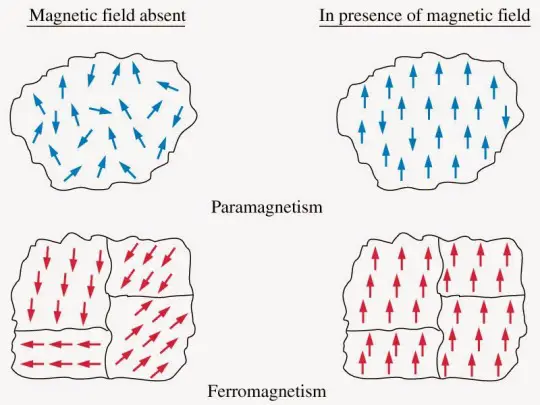
Unlike ferromagnets, paramagnets do not retain any magnetization in the absence of an externally applied magnetic field because thermal motion randomizes the spin orientations. (Some paramagnetic materials retain spin disorder even at absolute zero, which means they are paramagnetic in the ground state, i.e. in the absence of thermal motion.)
Thus the total magnetization drops to zero when the applied field is removed. Even in the presence of the field, there is only a small induced magnetization because only a small fraction of the spins will be oriented by the field.
This fraction is proportional to the field strength and this explains the linear dependency. The attraction experienced by ferromagnetic materials is non-linear and much stronger so that it is easily observed, for instance, in the attraction between a refrigerator magnet and the iron of the refrigerator itself.
Saturation magnetization value
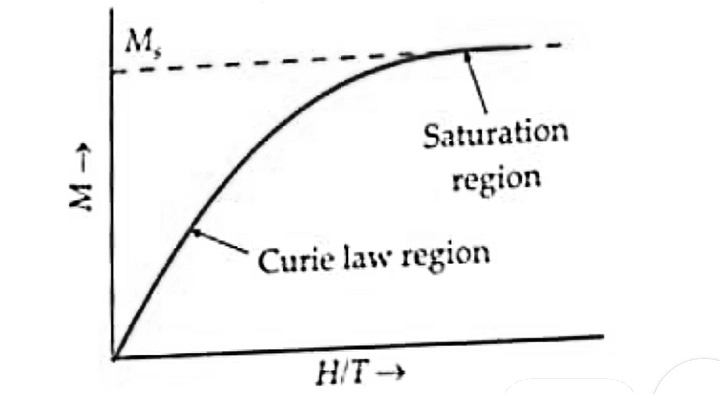
At a very high magnetic field or very low temperatures, the magnetization approaches maximum values when all the atomic dipole moments get aligned. This is called saturation magnetization value $M_s$.
Curie’s Law
From the experiment, it is found that the intensity of magnetization (M) of a paramagnetic material is
- Directly proportional to the magnetising field intensity (H), because the latter tends to align the atomic dipole moments.
- Inversely proportional to the absolute temperature T, because the latter tends to opposes the alignment of the atomic dipole moments.
Therefore, at low H/T values, we have
$$M\propto \frac{H}{T}$$ $$ Or \qquad M=C\cdot \frac{H}{T}$$ $$ Or \qquad \frac{M}{H}=\frac{C}{T}\quad or \quad \chi_m =\frac{C}{T}$$ Where, C is the Curie constant and $\chi_m$ is the magnetic susceptibility of the material. The above relation is called Curie’s Law.
Curie’s Law: This law states that far away from saturation, the susceptibility of a paramagnetic materials is inversely proportional to the absolute temperature (T).
Suggested reading:
- What is Magnetic permeability, relative permeability, and magnetic susceptibility? | Magnetism and matter class 12
- Classification of magnetic material with examples class 12
- What is Magnetic permeability, relative permeability, and magnetic susceptibility? | Magnetism and matter class 12
The following figure shows the variation of intensity of magnetization (M) as a function of $H/T$. Beyond the saturation value $(M_s)$, Curie’s Law is not valid.
Stay tuned with Laws Of Nature for more useful and interesting content.