The motion of a charged particle in a uniform electric field

In the previous article, we have studied the motion of charged particles in a uniform magnetic field. In this article, we will study the motion of charged particles in a uniform electric field. So let’s get started…

We will study the motion of charged particles in two ways-

• First, when there is no electric field.
• And second when there is an electric field.

When there is no electric field

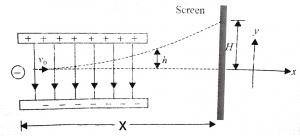
Consider the above figure and let’s assume that there is no electric field region between the plates. In this case, if you want to throw a negatively charged particle through the plates then the charged particle will follow a straight line trajectory along the x-axis because there are no external forces that will affect the motion of the charged particle. [latexpage]

In this motion, we can simply apply the laws of kinematics to study this straight motion.

Let’s consider a charged particle that is moving in a straight line with a constant velocity through the non-electric field region along X-axis. Let’s take the initial velocity of this negatively charged particle as $u_x$.

As the particle is moving with constant velocity along x-axis then the value of acceleration will be zero i.e $a_{x}=0$. From the second equation of motion, this motion can be mathematically depicted as-
$$S=ut+\frac{1}{2}a t^2$$
Now, it can be rewritten as follows:
$$x= u_{x}+\frac{1}{2}a_{x} t^2$$ Here, x is the distance traveled by the charged particle in x direction. But $a_{x}=0$, means $\displaystyle{\frac{1}{2}a_{x} t^2 =0}$
Now above equation becomes:
\begin{align*}
x&=u_{x}t\\
t&=\frac{x}{u_x}
\end{align*}

When there is electric field

This time, there is an electric field that is directed from positive charge to negative charge. See figure above. Now again if you want to throw the charged particle as you want to throw when there is no electric field. If you throw a charged particle this time then it will not follow the same path as it follows in no electric field region.

Since it is a negatively charged particle so, when it will move ahead it will keep attracting towards the positively charged plates because opposite charges attract each other. Therefore, the charged particle is moving in the electric field then the electric force experienced by the charged particle is given as-
$$F=qE$$
Due to its motion, the force on the charged particle according to the Newtonian mechanics is-
$$F=m a_{y}$$
Here, $a_{y}$ is the acceleration in the y-direction. As it is moving in the electric field, it keeps tilting towards the positive plates. Here, its motion is affected by the electric field, thus, it is not moving at a constant velocity. Its velocity will be increasingly changing (accelerates) if it is moving in the same direction as of electric field but if it is moving opposite of the direction of the electric field then its velocity will be decreasingly changing (de-accelerates).

Equating both forces, we get-
$$qE=m a_{y}$$
$$a_{y}=\frac{qE}{m}$$
From the second equation of motion, we get-
$$S=u_{y}t+\frac{1}{2}a_{y} t^2$$
Rewriting this equation
$$y= 0+\frac{1}{2} a_{y} t^2$$
Where y is the displacement in the y-direction. Here, $u_{y}$ is zero because the initial velocity in the y-direction is zero because we have thrown the particle along X-axis with the initial velocity $u_x$ due to the presence of the electric field, it is automatically tilted towards the y-direction. Note: we didn’t throw the particle in the y-direction. So here, we are taking $u_{y}$ as zero.
Putting the value of $a_{y}$ in above equation, we get-
$$y=\frac{qE t^2}{2m}$$
Also, putting the value of $t=\frac{x}{u_{x}}$, we have-
$$\boxed{y=\frac{qE x^2}{2m {u_{x}}^2}}$$
In this formula, the electric charge (q), electric field (E), mass of particle (m) and intial velocity in x-direction ($u_{x}$) all are constant, so we can rewrite the equation as follows:
$$ y=\left(\frac{qE}{2m {u_{x}}^2}\right)x^2$$
Therefore
$$\implies\qquad y\propto x^2$$
$$y=Kx^2$$
$$\text{where,}\quad K=\frac{qE}{2m {u_{x}}^2}$$
This equation is the same as the equation of the parabola, it means the motion of the charged particles in the uniform electric field follows a parabolic path.

Stay tuned with Laws Of Nature for more useful and interesting content.