In this short piece of article, we will discuss what is magnetic flux? definition, formula, units, and its dimensions, so let’s get started…
What is magnetic flux?
Magnetic flux definition: The magnetic flux through any surface placed in a magnetic field is the total number of magnetic lines of force crossing this surface normally. It is measured as the product of the component of the magnetic field normal to the surface and the surface area.
Read Also
- Electric flux: basic concepts, definition, formula, unit, symbols, electrostatic class 12
- Magnetic field and, properties of magnetic field lines, class 12.
Magnetic flux symbol
- Magnetic flux is a scalar quantity. It is usually denoted by the Greek letter $\phi$ or $\phi_B$
- Magnetic flux symbol: $\phi$ or $\phi_B$.
Magnetic flux formula
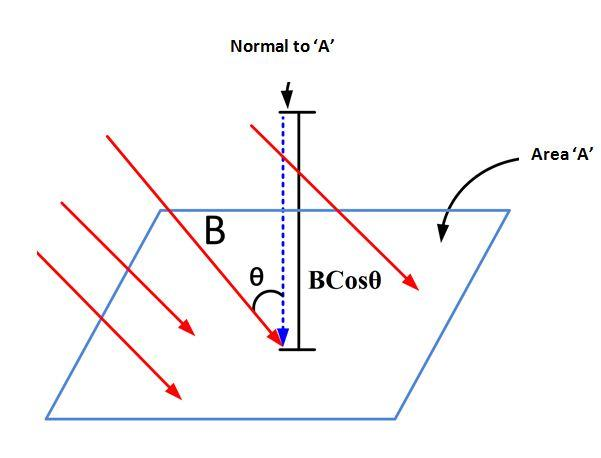
If a uniform magnetic field $\overrightarrow{B}$ passes normally through a plane of the area $A$. See the figure below, then the magnetic flux through this area is given as $$\phi = BA$$
If the magnetic field $\overrightarrow{B}$ makes an angle $\theta$ with the normal drawn to the area $A$, See the figure below, then the component of the field normal to this area will be $B\cos\theta$, therefore the magnetic flux is given as $$\phi = B\cos\theta\times A$$ $$Or\qquad \boxed{BA\cos\theta=\overrightarrow{B}\cdot \overrightarrow{A}}$$ Here, the direction of the vector $A$ is the direction of the outward drawn normal to the surface.
Derivation of the magnetic flux for the small area dA
The magnetic field $\overrightarrow{B}$ over an area $A$ is may not be uniform but $\overrightarrow{B}$ over a small area $d\overrightarrow{A}$ can be assumed to be uniform. See the figure below, if the magnetic lines of force pass through the area element $d\overrightarrow{A}$ with an angle $\theta$ with its normal vector, then the component of the $\overrightarrow{B}$ normal to the $d\overrightarrow{A}$ is $B\cos\theta$.
Magnetic flux through an area element $d\overrightarrow{A}$ is given as $$d\phi=B_\perp dA = B\cos\theta \;dA$$ $$=B\;dA\cos\theta = \overrightarrow{B}\cdot d\overrightarrow{A}$$
Magnetic flux through the whole area $A$ is $$\phi=\int_A B\cos\theta \;dA = BA\cos\theta$$
Dimension of magnetic flux
As we know that $$\phi = BA$$ But $$B=\frac{F}{qv\sin\theta}\quad \therefore\quad \phi= \frac{F}{qv\sin\theta}\cdot A$$ Dimension of the magnetic flux: $$\begin{aligned}\phi &= \frac{MLT^{-2}}{CLT^{-1}.1}\cdot L^2\\&=\frac{ML^2 T^{-2}}{A}\qquad [\therefore 1CT^{-1}=1A]\\\phi&=[ML^2 T^{-2}A^{-1}]\end{aligned}$$
SI unit of magnetic flux
The SI unit of magnetic flux is weber (Wb). One weber is the magnetic flux produced when the magnetic field of one-tesla acts normally over an area of 1 m2. $$1\text{weber}=1\text{tesla}\times 1\text{meter}^{2}$$ $$\text{Or,}\qquad 1Wb=1Tm^2$$
CGS unit of magnetic flux
The CGS unit of magnetic flux is Maxwell (Mx). One Maxwell is the magnetic flux produced when the magnetic field of one gauss acts normally over an area of 1 cm2. $$1\text{Maxwell}=1\text{gauss}\times 1\text{cm}^{2}$$ $$\text{Or,}\qquad 1Mx=1G{cm}^2$$
Relation between weber and maxwell
| $$1Wb=1T\times 1m^2=10^4G\times 10^4 {cm}^2$$ $$1Wb=10^8 \text{maxwell}$$ |
Positive and negative flux
The normal can be drawn on either side of the area, if
Positive flux: If the normal is drawn to the area points in the direction of the field, $\theta = 0^{\circ}$ then the flux is taken as positive.
Negative flux: If the normal is drawn to the area points in the opposite direction of the field, $\theta = 180^{\circ}$ then the flux is taken as negative.
Stay tuned with Laws Of Nature for more useful and interesting content