Here, we will derive an expression for magnetic field due to a toroid. So lets get started… Wait before getting started, let’s recall what is a toroid?
WHAT IS A TOROID?
A toroid is just a circular solenoid (doughnuts shaped) whose both ends are joined together. Generally, a toroid is a circular hollow ring on which several copper wires are wrapped closely with no gaps between the turns.
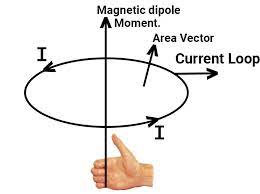
When electric is flows inside the toroid, it produces magnetic field like solenoid. The magnetic field is zero inside and outside the toroid. Inside the toroid, the magnetic field is along with the circular turn and it is constant in magnitude and its direction is clockwise inside the toroid as per the right-hand thumb rule for circular loops.
DERIVATION FOR MAGNETIC FIELD DUE TO A TOROID
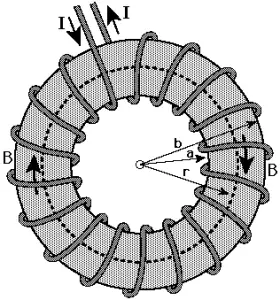
We know that magnetic field inside (central section of toroid) and outside of the toroid is zero. Magnetic field is found only inside the torus of the toroid, means circular hollow region of the toroid on which coils are bounded.[latexpage]
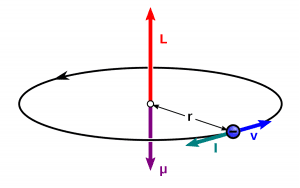
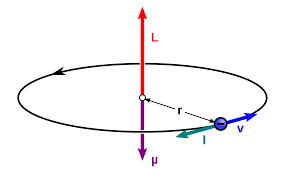
Let’s consider a toroid having N turns of coils and I current is flowing through it. Take a arbitrary point P inside the toroidal region whose distance is r from the centre of the toroid.
Using that radius/distance make a circular amperian loop. See figure above, dotted circle is the amperian loop with radius r. Consider that this amperian loop is enclosing the current I. Then, from the ampere’s circuital law:
\begin{align*}
\oint\mathbf{B}\cdot d\mathbf{l}&=\mu_0 NI\\
\oint\mathbf{B} d\mathbf{l}\; cos{0}^{\circ}&=\mu_0N I\\
\mathbf{B}\oint d\mathbf{l}&=\mu_0 NI\\
\mathbf{B} 2\pi r& =\mu_0N I\\
B&=\frac{\mu_0N I}{2\pi r}
\end{align*}
$$\quicklatex{size=20}\boxed{B=\mu_0 nI}$$
Where n is the numbers of turns per unit length, i.e $\displaystyle{n=\frac{N}{2\pi r}}$
SPECIAL CASES
1). If the point is inside the central toroidal space – If we take a arbitrary point P inside the hollow central part of the toroid then in this case magnetic field is zero at that point. It is because if we draw a amperian loop with radius (a), see figure above: then this loop wouldn’t encloses any electric current and hence magnetic field (B) will be zero.
\begin{align*}
\oint\mathbf{B}\cdot d\mathbf{l}&= 0\\
B&=0
\end{align*}
2). If the point is inside the toroid – If we take a arbitrary point P inside the torus of the toroid and then magnetic field wouldn’t be zero because if we draw a amperian loop with radius r then it encloses the current I.
$$\oint\mathbf{B}\cdot d\mathbf{l}=\mu_0 NI$$
3). If the point is outside the toroid – If we take a arbitrary point P outside the toroid then in this case magnetic field is zero at that point. It is because if we draw a amperian loop with radius (b), see figure above: then this loop wouldn’t encloses any net electric current and hence magnetic field (B) will be zero.
Stay tuned with Laws Of Nature for more useful and interesting content.