Lorentz force
Introduction
In this present article, we will talk about the force acting on the charged particle when it moves in a simultaneous electric and magnetic field. The electromagnetic force experienced by the moving charged particles due to the simultaneous presence of electric and magnetic fields is finally derived by the Dutch physicist Hendrik Antoon Lorentz in the year 1895.
The derived formula is considered as the modern form of the formula for the electromagnetic force which includes the total force from both the electric and the magnetic fields.
Lorentz force definition
| Especially in electromagnetism, the Lorentz force (or electromagnetic force) is the combination of the electric and magnetic force on a point charge due to the presence of electromagnetic fields. |
If a positive charge particle q moving with a velocity v in an electric field E and a magnetic field B then it experiences a force given by- [latexpage]
$$\displaystyle \mathbf {F} =q\,\mathbf {E} +q\,(\mathbf {v} \times \mathbf {B})$$
This formula is called Lorentz force. According to this formula, the Lorentz force on a charged particle q is the combination of the electric force and magnetic force.
The electric force will be in the same direction as of the electric field E and it is given as the product of electric charge q and the magnitude of the electric field (E), and the magnetic force is at right angles to the magnetic field (B) and the velocity (v) of the charged particle, and it is given as the product of electric charge q to the cross product of field B and the velocity v. See expression above.
Lorentz force as the definition of electric and magnetic field
The Lorentz force law can be used as a definition of the electric and magnetic fields E and B. In particular, the Lorentz force can be understood from the following empirical statement:
| The electromagnetic force F on the test charge at a given point and time is a particular function of the charge q and its velocity v, which can be precisely parameterized by two vectors E and B as a function, as shown below- $${\displaystyle \mathbf {F} =q(\mathbf {E} +\mathbf {v} \times \mathbf {B} )}$$ |
This expression is valid even for the particles whose velocity is approaching the speed of light. So, two vector fields E and B are defined in all space and time, and they are called “electric field” and “magnetic field“.
The fields are determined throughout space and time depending on the strength that the test charge will receive regardless of the presence of a charge to experience the strength.
As a definition of the electric and magnetic field, the Lorentz force is only a principle definition because a real particle (in contrast to the hypothetical “test charge” of infinitely small mass and charge) would generate its own finite electric and magnetic fields, which it would change the electromagnetic force that it experiences.
If the charged particle goes in acceleration then the particle is forced into a curved trajectory and it starts emitting electromagnetic radiation that causes to loss of Kinetic energy. See, Bremsstrahlung and synchrotron light. These effects occur directly through a direct effect (radiation reaction force) and indirectly (by influencing the movement of neighboring charges and currents).
Lorentz force formula
Lorentz force formula in terms of charged particle

Let a charged particle q moving in the simultaneous presence of electric and magnetic field with the instantaneous velocity of v then the Lorentz force F experienced by the charged particle q due to an external electric field E and magnetic field B, is given by-$${\displaystyle \mathbf {F} =q\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right)}$$
In the above formula × is the vector cross product and all the quantities you see in boldface letters are vectors. In terms of Cartesian components, the lorentz force can be given as-
\begin{equation*}
\begin{split}
F_{x}&=q\left(E_{x}+v_{y}B_{z}-v_{z}B_{y}\right),\\
F_{y}&=q\left(E_{y}+v_{z}B_{x}-v_{x}B_{z}\right),\\
F_{z}&=q\left(E_{z}+v_{x}B_{y}-v_{y}B_{x}\right)
\end{split}
\end{equation*}
In general, the electric and magnetic fields are always been a function of position and time because their value can be different for different positions and times. So, explicitly, the Lorentz force can be given as:
$$
{\displaystyle \mathbf {F} \left(\mathbf {r} ,{\dot {\mathbf {r} }},t,q\right)=q\left[\mathbf {E} (\mathbf {r} ,t)+{\dot {\mathbf {r} }}\times \mathbf {B} (\mathbf {r} ,t)\right]}
$$
Where
- r is the position vector of the charged particle
- t is the time
- and the raised dot over the letter denotes the derivative w.r.t time.
When a positively charged particle moves in the electric field then it accelerates in the same direction as the electric field, but when it moves in the region of the magnetic field then it becomes perpendicular to both the instantaneous velocity vector v and the magnetic field B according to the right-hand rule.
| Right-hand rule:
Extend your right hand’s thumb, index, and middle finger such that they are perpendicular to each other, see figure below: 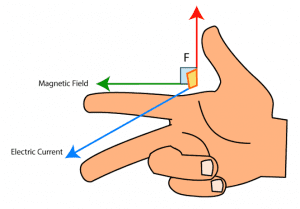 Now align your extended fingers such that the middle finger points the direction of particle velocity v, the index finger points the direction of the magnetic field B, then your extended thumb will automatically point the direction of magnetic force F. |
The term qE is called the electric force, while the term q(v × B) is called the magnetic force. In some text “Lorentz force” is specifically considered as the empirical formula for magnetic force (including electric force).
The magnetic force component of the Lorentz force can change itself to give a force that acts on a current-carrying wire in a magnetic field. In that context, this Lorentz force is also called the Laplace force.
$$\displaystyle{qvB=It\,\frac{l}{t}B=lIB}$$
where $\displaystyle{lIB}$ is the force acting on the current-carrying wire in a magnetic field.
So the Lorentz force is a force that is exerted by the electromagnetic field (by the presence of electric and magnetic field) on the charged particle, in terms of momentum it is defined as the rate at which linear momentum is transferred from the electromagnetic field to the particle. Or in terms of power, it is defined as the rate at which energy is transferred from the electromagnetic field to the particle. That power is given as-
$$
{\displaystyle \mathbf {v} \cdot \mathbf {F} =q\,\mathbf {v} \cdot \mathbf {E} .}$$
Caution: magnetic field does not contribute to the power because the magnetic force is always perpendicular to the velocity of the charged particle and hence, resultant work done is always zero.
Lorentz force formula in terms of continuous charged distributions
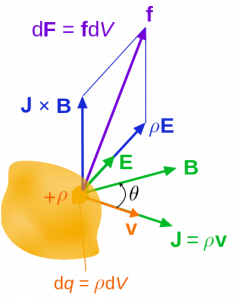
For a body of continuous charge distribution in motion, the Lorentz force formula can be given as-
$${\displaystyle \mathrm {d} \mathbf {F} =\mathrm {d} q\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right)\,\!}$$
where ${\displaystyle \mathrm {d} \mathbf {F}}$ is the force acted on a small piece of the charge distribution with charge ${\displaystyle \mathrm {d} q}$. If both sides of this formula are divided by the volume of this small piece of the charge distribution ${\displaystyle \mathrm {d}\mathbf{V}}$, then it becomes-
$${\displaystyle \mathbf {f} =\rho \left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right)\,\!}$$
where ${\displaystyle \mathbf {f} }$ is the force density (force per unit volume) and ${\displaystyle \rho }$ is the charge density (charge per unit volume). Now the current density of the corresponding motional charge continuum is-
$$\mathbf {J} =\rho \mathbf {v}$$
Substitute this current density formula in the formula of force density above, then we get-
$$
{\displaystyle \mathbf {f} =\rho \mathbf {E} +\mathbf {J} \times \mathbf {B} \,\!}$$
So, the total Lorentz force acted on the body of continuous charge distribution is the volume integral over the charge distribution and it is given as-
$$
{\displaystyle \mathbf {F} =\iiint \!(\rho \mathbf {E} +\mathbf {J} \times \mathbf {B} )\,\mathrm {d} V}$$
Significance of Lorentz force
Modern Maxwell’s equations can describe how moving charge and current carriers or charge carriers create electric and magnetic fields. Lorentz’s law of force completes this picture by describing the force acting on a point charge moves q in the presence of an electromagnetic field.
Lorentz’s law of force describes the effects of electric field E and magnetic field B on point charges, but such electromagnetic forces are not the complete picture.
Charged particles can combine with other forces, especially gravity and nuclear force. Consequently, Maxwell’s equations are inseparable from other laws of physics, and they are combined with them through charge and current densities.
The response of a point charge to Lorentz’s law is one aspect but generating electric and magnetic fields by charges and current is another matter. In real materials, the Lorentz force is insufficient to describe the collective behavior of charge carriers, both in principle and from a computational point of view.
Charged particles in the physical environment react to the fields E and B and create these fields. To determine the temporal and spatial response of the charges, it is necessary to solve complex transport equations, for example, the Boltzmann equation, the Fokker-Planck equation, or the Navier-Stokes equation.
For more details, see magnetohydrodynamics, electrohydrodynamics, superconductivity, stellar evolution. Some physical apparatus such as the green’s Kubo reaction and greens function (many-body theory) has been developed for dealing with this type of matter.
Applications of Lorentz force
The concept of Lorentz force is used in many daily use devices. Some applications of Lorentz force is listed below:
- It is used in a cyclotron and other particles accelerators.
- Used in a mass spectrometer
- Velocity filters
- Magnetrons
- Used in Lorentz force velocimetry.
On the manifestation Lorentz force as the Laplace force on the current-carrying wire. This force is used in many devices such as:
- Electric motors
- Railguns
- Linear motors
- Loudspeakers
- Magnetoplasmadynamic thrusters
- Electrical generators
- Homopolar generators
- Linear alternators
Watch this video for more visual understandings.
So this is all about Lorentz force, stay tuned with Laws Of Nature for more useful and interesting content.







Thanks for sharing the best information. I am really enjoying reading your well-written articles.