In this article we are going to talk about electric potential energy and further we will derive an expression for electric potential energy of a system of two point charges. So keep reading..

ELECTRIC POTENTIAL ENERGY

Do you remember the definition of electric potential? which we have talked in earlier section. In the privious section, we have defined electric potential as follows:

Electric potential is defined as the amount of work done in bringing the unit positive test charge from infinity to a point against the electric field without any acceleration. Mathematically it is given as –
[latexpage]
$$
V=\frac{W}{q_0}
$$
Well this is the formula for electric potential but what’s about this work done, which is used to move a positive test charge or a system of charges?. where does this energy stored and in what form? And what we called this energy?

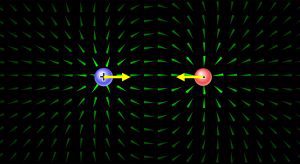
This work done is nothing but the electric potential energy. This amount of work done (which is used in bringing a unit positive test charge from infinity to a specific point in electric field) is stored in electrical bodies or charges as electrical potential energy.

The electric potential energy of any given point charge or system of charges is defined as the total work done by an external agent in bringing the charge or the system of charges from infinity to the present configuration without going to any acceleration.

An object may have electric potential energy by virtue of its two key elements: first is its own electric charge and second is it’s relative position of with the others electric charges. This statement will be more clear after the derivation for electric potential energy.

DERIVATION FOR ELECTRIC POTENTIAL ENERGY

Consider two point charges $q_1$ and $q_2$ lying at points A and point B,and whose location are $r_1$ and $r_2$ respectively.

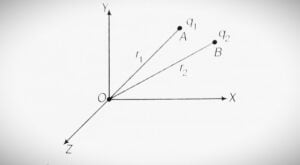
To find the electric potential energy of this two charge system, then we have to thought for a system in which both charges are infinitely far away and at rest. Now we will bring each charges one by one. First, $q_1$ is brought from infinity to the point $r_1$. While bringing first charge, we see that there is no any external electric field against which work to be done, so work done in bringing charge $q_1$ from infinite to $r_1$ is zero.

After placing charge $q_1$ at point A, a electric potential V is set up at point B, where $q_2$ charge is to be placed. Electric potential at point B due to charge $q_1$ is given as-
$$
V=\frac{1}{4\pi\epsilon_0}\frac{q_1}{r_{AB}}
$$
Where $r_{AB}$ is the distance between A and B. By definition, work done in bringing charge $q_2$ from infinite to point B is-
\begin{align*}
W&=\text{potential} \times \text{charge}\\
W&=\frac{1}{4\pi\epsilon_0}\frac{q_1}{r_{AB}}.{q_2}
\end{align*}
Since,the electric potential energy $U_E$ is the work done in bringing the charge $q_2$ at the point B, which is in the electric field region of charge $q_1$ and points which is seperated by the distance of $\displaystyle{r_{AB}}$ is given as-
$$
U_E=W=\frac{1}{4\pi\epsilon_0}\frac{q_1q_2}{r_{AB}}
$$

IMPORTANT CASES REGARDING POTENTIAL ENERGY

• IF $q_1$ AND $q_2$ BOTH ARE GREATER THAN ZERO- If both charges are greater than zero, then electric potential energy increases if we brought both charges closer, and it decreases if we take away the both of the electric charges. It happens because when we brought both charges closer to each other then the work is done against the force of repulsion. In this case work is done on the system. Which is stored as positive potential energy in the charges. But on the other hand, if we take away both of the charges then work is done by the system and they started loosing the energy.
• IF THEY ARE OPPOSITEVELY CHARGED- If they are oppositevely charged then they will be show attraction. If we move the electric charges in the the direction of attraction then the electric potential energy decreases because work is done by the system, but if move the electric charges in the opposite direction of their attraction then the electric potential energy increases because work is done on the system.

Watch this video for more reference:

FREQUENTLY ASKED QUESTIONS

1).What is meant by electric potential energy?

Ans- Potential energy is the amount of work required to move a charge against the electric field without undergoing in any acceleration.

2). How do you find electric potential energy?

Ans- If you want to find the value of potential energy then you are free to use this formula.
\begin{align*}
W&=Vq\\
W&=\frac{1}{4\pi\epsilon_0}\frac{q_1q_2}{r}
\end{align*}
Where $q_1$ and $q_2$ are charges and r is their seperation distance.

3). Why is electric potential energy negative?

Ans- If both charges are like (eg. +,+ or -,-) then potential energy will be negative. It is because we have to do work against the electric field in moving the charges closer and apart.