In this article, we are going to derive an expression for potential energy of a system of three points charges. So keep reading till end..

DERIVATION FOR THE POTENTIAL ENERGY OF A SYSTEM OF THREE POINTS CHARGES

$latexpage$
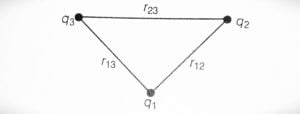
Let’s consider a system of three points charges $q_1$, $q_2$ and $q_3$ having position vector $r_1$, $r_2$ and $r_3$ respectively from the origin as shown in following figure.

If we bring charge $q_1$ first from infinity to position $r_1$ then there is no work done required to do so, it is because when we bring charge $q_1$ from infinity to position $r_1$ then at that position there is no any source which can produce electric field. If there is no electric field then there is no any opposing force. Hence work done is zero.
$$\therefore W_1=0$$
But when we bring charge $q_2$ from infinity to the position $r_2$ then in this, we have to do work done because, here a opposing field is present due to charge $q_1$. So we have to do work done in against the electric field produced by the first electric charge $q_1$.
The work done in bringing charge $q_2$ from infinity to the position $r_2$ is-
$$\begin{align*} W_2&=q_2V\left(r_2\right)\\ W_2&=\frac{1}{4\pi\epsilon_0}\frac{q_1q_2}{r_{12}} \end{align*}$$
Where $r_{12}$ is the position vector between charge $q_1$ and $q_2$ and V is the electric potential due to charge $q_1$ at position vector $r_{12}$.
Now, charges $q_1$ and $q_2$ will produce a electric potential at any point say P. Think that point P denotes the position of charge $q_3$. The position vector between charge $q_1$ and $q_3$ will be $r_{13}$ and in between charge $q_2$ and $q_3$ will be $r_{23}$.

Now the electric potential due to the charge $q_1$ and $q_2$ at point P is given as-
$$V_{1,2}=\frac{1}{4\pi\epsilon_0}\left(\frac{q_1}{r_{13}}+\frac{q_2}{r_{23}}\right)$$
So the work done in bringing charge $q_3$ from infinity to the position $r_3$ is-
$$\begin{align*} W_3&=q_3V_{1,2}\left(r_3\right)\\ &=\frac{1}{4\pi\epsilon_0}\left(\frac{q_1q_3}{r_{13}}+\frac{q_2q_3}{r_{23}}\right) \end{align*}$$
The total work done in assembling the charges at the given location is equal the total potential energy of the system and According to the superposition principle, this total potential energy can be obtained by adding the work done of individual charges.
$$\begin{align*} U&=W_1+W_2+W_3\\ &=0+\frac{1}{4\pi\epsilon_0}\frac{q_1q_2}{r_{12}}+\frac{1}{4\pi\epsilon_0}\left(\frac{q_1q_3}{r_{13}}+\frac{q_2q_3}{r_{23}}\right) \end{align*}$$
$$\boxed{U=\frac{1}{4\pi\epsilon_0}\left(\frac{q_1q_2}{r_{12}}+\frac{q_1q_3}{r_{13}}+\frac{q_2q_3}{r_{23}}\right)}$$
This result can also be expressed in the form of summation as follows-
$$U=\left[\frac{1}{4\pi\epsilon_0}\sum_{i=1}^3\sum_{i=1_{j\neq i}}^3\frac{q_iq_j}{r_{ij}}\right]$$
If we want to obtain the value of electric potential energy of a system of N point charges then we also obtained it. The value of electric potential energy due to a system of N point charges is equal to the total amount of work done in assembling all the charges to the given position from infinity.
$$\begin{align*} U&=\left[\frac{1}{4\pi\epsilon_0}\sum_{i=1}^N\sum_{i=1_{j\neq 1}}^Nq_iV_j\right]\\ \text{where}\; V_j&=\sum_{i=1_{j\neq i}}^N\frac{1}{4\pi\epsilon_0}\frac{q_i}{r_{ij}} \end{align*}$$
Watch this video for more reference:

We know that electrostatic force is conservative in nature, so the value of U is independent of the manner in which the configuration of charge is assembled.
The SI unit of electric potential energy is joule (J) and it’s another unit is electron volt (eV)
$$\begin{align*} 1eV&=1.6\times10^{-19}\times1V\\ &=1.6\times10^{-19}J \end{align*}$$