In this article, we are going to derive an expression for electric potential energy of an electric dipole in external electric field. So keep reading…
ELECTRIC POTENTIAL ENERGY OF AN ELECTRIC DIPOLE IN EXTERNAL ELECTRIC FIELD
Let’s take a electric dipole of charges +q and -q and have a seperation distance of 2a is placed in a uniform external electric field of magnitude E. When a dipole in placed in a uniform external electric field it experiences a electric force of magnitude +qE and -qE which is equal and opposite to each other.
We know that if any electric dipole placed in uniform external electric field then the both charges as a whole does not experience any net force on the system, which can be seen in the following figure.
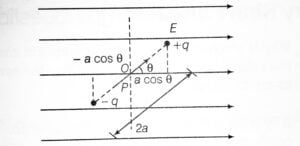
It is true that it doesn’t experience any net force but it experiences a torque (τ) which can be given as-
[latexpage]
$$
\tau=p\times E
$$
This torque rotates the electric dipole unless it align parallel or antiparallel to the electric field. If we apply an external torque $\left(\tau_{ext}\right)$ to neutralize the effect of torque of this electric dipole. Then we have to do work done in oppose of this torque.
Suppose an external $\left(\tau_{ext}\right)$ is applied to the dipole, so that, it rotates from angle $\theta_0$ to $\theta_1$ with respect to the electric field E.
DERIVATION FOR ELECTRIC POTENTIAL ENERGY
The amount of work done in neutralizing the effect of torque of the electric dipole is given by-
\begin{align*}
W&=\int_{\theta_0}^{\theta_1}\tau_{ext}\theta d\theta\\
&=\int_{\theta_0}^{\theta_1}pE\sin\theta d\theta\\
W&=pE\left[-\cos\theta\right]_{\theta_0}^{\theta_1}\\
W&=pE\left(\cos\theta_0-\cos\theta_1\right)
\end{align*}
This work done W is stored as electric potential energy in the system of electric dipole. Therefore, the electric potential energy in the electric dipole placed in the external electric field is given as-
$$
\boxed{U\left(\theta\right)=pE\left(\cos\theta_0-\cos\theta_1\right)}
$$
IMPORTANT CASES
1). If a electric dipole is initially aligned along the electric field, i.e $\theta_0=0$, and we want to set it at angle $\theta$ with the electric field, i.e $\theta_1=\theta$
\begin{align*}
\therefore W&=pE\left(\cos\theta_0-\cos\theta_1\right)\\
W&=pE\left(\cos0^{\circ}-\cos\theta\right)\\
W&=pE\left(1-\cos\theta\right)
\end{align*}
This work done is stored in the electric dipole in the form of electric potential energy.
2). When the dipole is initially at right to E, i.e $\theta_0=90^{\circ}$ and wanted to set at angle $\theta$ with E, i.e $\theta_1=\theta$
$$
W=pE\left(\cos90^{\circ}-\cos\theta\right)=-pE\cos\theta
$$
Potential energy of the dipole,$U=W=-pE\cos\theta$
$$
U=-pE\cos\theta
$$
Electric potential energy of the electric dipole is a scalar quantity an it is measured in joule (J).
SOME IMPORTANT RESULTS
1). Electric potential at any point on the bisector of electric dipole is zero.
2). If electric field is non – uniform then the the net force on the electric dipole is in the direction of electric field.
3). A electric dipole experience maximum torque at the position where it’s potential energy is zero.
Watch this video for more reference:
FREQUENTLY ASKED QUESTIONS
1). What is the potential energy of a dipole in a uniform electric field?
Ans- The potential energy of an electric dipole in uniform external electric field is the work done by the external torque to neutralize the effect of torque of the electric dipole. This work done is given as-
$$
U=W=-pE\cos\theta
$$
2). What happens to a dipole in a non uniform electric field?
Ans- If a dipole in a non uniform external electric field then the dipole experience a net electric force and as well as torque.
3). For what orientation does an electric dipole experience a zero torque but non zero force in a non uniform electric field?
Ans- When electric dipole is parallel or antiparallel to the electric field.
4). What is non uniform electric field?
Ans- If the value of electric field has same magnitude and direction at every point in the given space then it is called uniform electric field. But if either magnitude or direction or both changes then it is called non uniform electric field in that given space.