POTENTIAL ENERGY OF AN ELECTRIC DIPOLE

[latexpage]

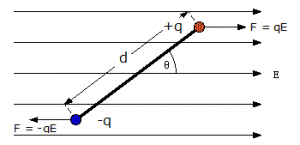
Let’s take a electric dipole of charges +q and -q and the seperation distance between their charge is d. Imagine that this electric dipole is placed into a region of uniform electric field E. As we know that when we place a electric dipole in uniform external electric field then it start experiencing a torque(τ). Which can be given as-
\[
\tau = p\times{E}
\]
This torque creates due to the formation of couple. Couple formed when two forces are equal in magnitude and opposite in direction acts in different points perpendicularly.

Due to this torque electric dipole starts rotating. This torque rotates the dipole untill it is placed parallel or anti-parallel to the electric field. Dipole rotates untill it is placed parallel or anti-parallel to the electric because this is the equilibrium position of the dipole. At this position dipole doesn’t experience any torque due to the electric field. Every electric dipole when it placed in external electric field then it starts experiencing Torque and due to this it tries to align in such a way to attain stable equilibrium.

What will happen If we apply an external and opposite torque? If we apply external and opposite torque then it neutralizes the effect of this torque and it given as $\tau_{ext}$ and it rotates the dipole from the angle $\theta_0$to an angle $\theta_1$ at an infinitesimal angular speed without any angular acceleration.

DERIVATIONS FOR THE POTENTIAL ENERGY

Potential energy of a dipole is the energy possessed by the dipole by virtue of its particular position in the electric field.

As we have discussed above that when we apply external and opposite torque on the electric dipole then it’s neutralize the effect of this torque and it rotates the dipole from the angle $\theta_0$ to an angle $\theta_1$ at an infinitesimal angular speed without any angular acceleration.

When we are applying external and opposite torque on the dipole then in the form of this, what we are doing? We are doing just work done. Means we have to do work done in order to rotates the dipole from the angle $\theta_0$ to an angle $\theta_1$. This work done stored in the electric dipole in the form of potential energy.

Small amount of work done in rotating the electric dipole through a small angle dθ against the torque is –
$$
dW = \tau{d\theta}=pE\sin\theta{d\theta}
$$
Total work done in rotating the dipole from orientation $\theta_0$ to $\theta_1$ is-
\begin{align*}
W&=\int_{\theta_0}^{\theta_1}pE\sin\theta{d\theta}\\
&=pE\left(\cos\theta_0-cos\theta_1\right)
\end{align*}
Let’s assume that dipole is initially oriented at angle $\theta$ to the direction of electric field. After applying some external and opposite torque it orientation changed by making angle 90° to the direction of the electric field. Then the work done-
\begin{align*}
W&=pE\left(\cos{90^{\circ}}-{\cos\theta}\right)\\
W&= -pE\cos\theta\\
W&= -p.E
\end{align*}
The potential energy of the electric dipole is a scalar quantity and it is measured in joule.