Bar magnet as an equivalent solenoid
In this article, we are going to discuss how does a bar magnet is equivalent to a solenoid? In order to understand this equivalency, we have to take a brief knowledge about solenoid and bar magnets. So let’s get started…
What is a bar magnet?
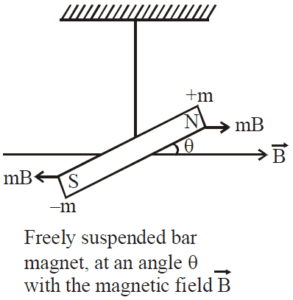
A bar magnet is a rectangular piece of an object, that is made up of iron, steel, cobalt, or any other ferromagnetic substance. It shows permanent magnetism. It has two poles, a north, and a south pole. When a bar magnet is suspended freely via inextensible thread, then the magnet tends to align itself so that the north pole of the bar magnet points towards the magnetic south pole of the earth. [latexpage]
Suggested reading:
What is a solenoid?
A solenoid is a helical coil that can be obtained by tightly bounding the copper wire on the cylindrical portion of the insulating material. When electric current flows through the solenoid, it creates a magnetic field.
Suggested reading:
Derivation of Bar Magnet as an Equivalent Solenoid
To show that a bar magnet is equivalent to a solenoid. We can find the magnetic field at the axial line of a finite current-carrying solenoid. If the derived formula of the magnetic field is the same as the formula for the magnetic field at the axial line of a bar magnet then it can be demonstrated as a solenoid.
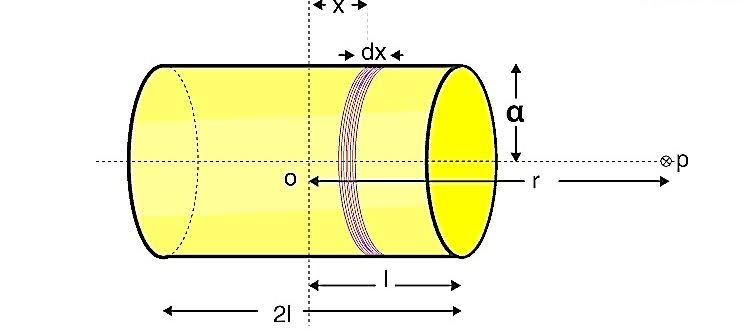
Consider a solenoid of radius $a$ and length $2l$ with $n$ number of turns per unit length that has current $I$ passing through the solenoid. Considering a small element of thickness $dx$ of the solenoid at distance $x$ from $O$ such that $OP = r$.
Magnetic field due to $n$ turns of a solenoid at the point $P$ on the axial line is – $$dB=\frac{\mu _{0}ndxIa^{2}}{2\left [ (r-x)^{2}+a^{2} \right ]^{\frac{3}{2}}}$$
If $P$ lies at a very large distance from $O$, i.e. $r>>>>a$ and $r>>>>x$, then $$[(r-x)^2+a^2]^{\frac{3}{2}} \approx r^3$$
Integrating $x$ from $-l$ to $+l$ to get the magnitude of the total magnetic field. $$B=\frac{\mu _{0}nIa^{2}}{2r^3}\int_{-l}^{l}{dx}$$ $$=\frac{\mu _{0}n2l}{2}\frac{Ia^{2}}{r^{3}}$$ Therefore, magnetic field at axial line of a solenoid is given as: $$B=\frac{\mu _{0}}{4\pi }\frac{2m}{r^{3}}$$ We see that magnetic field due to a solenoid at axial line is same as the formula of magnetic field at axial point of a bar magnet. So we can say that bar magnet is equivalent to a solenoid.
Similarities between a current carrying solenoid and a bar magnet
When current is passed through a solenoid it behaves like a bar magnet. Some observations are given below which show the similarities between a current-carrying solenoid and a bar magnet.
- When a current carrying solenoid is suspended freely it always come to rest at North South direction as like bar a magnet.
- When two different current-carrying solenoid brought closer to each other they exhibit mutual repulsion and attraction. This mutual repulsion and attraction shows that their end faces acts as N-pole and S-pole as like of a bar magnet.
- Magnetic field is same for both at axial point.
- They have the same magnetic dipole moment.
- When a compass needle brought near a current carrying solenoid, it shows deflection in a same way as shows in the case of bar magnet.
- The pictorial representation of magnetic field lines is same for the Solenoid and a bar magnet.
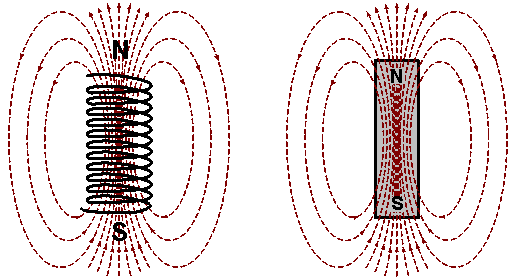
Difference between solenoid and a bar magnet
Some differences between a solenoid and a bar magnet are as follows:
- The bar magnet is a permanent magnet whereas a solenoid is an electromagnet. A solenoid acts as a magnet only when an electric current is passed through it.
- When a bar magnet is cut into two halves, both the pieces act as a magnet with the same magnetic properties whereas when a solenoid is cut into two halves, their magnetic properties become lowered because it’s magnetic is depends on the number of turns of the coils.
- Poles of a bar magnet are fixed whereas poles of a solenoid can be altered.
- Magnetic field due to a bar magnet didn’t depends on the magnitude of electric current whereas for a solenoid it does.
How does a solenoid equivalent to a bar magnet
According to the current loop as a magnetic dipole
We can consider a solenoid as a combination of circular rings placed side by side as shown in the following figure. Each circular ring or loop of a solenoid is regarded as a magnetic dipole having a magnetic moment $IA$.
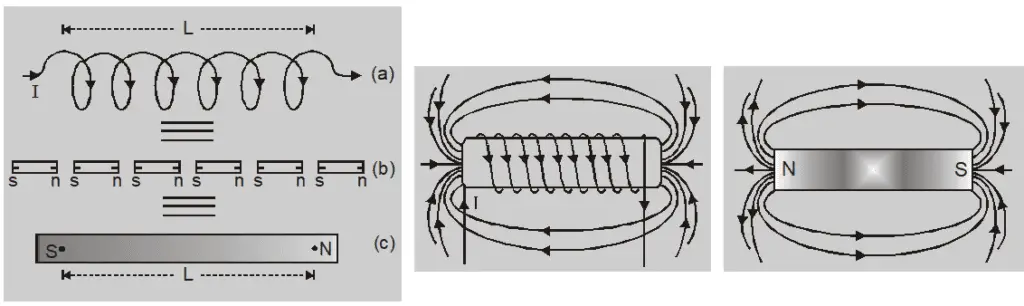
So a solenoid is taken as an arrangement of small circular rings (magnetic dipole) which is placed in line with each other to a finite length. The numbers of these magnetic dipoles are equal to the number of turns in the solenoid. These magnetic dipoles are arranged such that the north pole of one touches the South pole of the adjacent one. The opposite side neutralizes each other except the ends.
Thus, a current-carrying solenoid can be replaced by a single south pole and north pole bar magnet, separated by some distance equal to the length of the solenoid. Hence, a current-carrying solenoid is equal to a bar magnet.
According to the Ampere’s hypothese
We can also explain the equivalency of the bar magnet to the solenoid by Ampere’s hypotheses. According to ampere’s hypotheses, all magnetic effects are produced by the current loop. We know that the electrons keep revolving around the nucleus and hence electric current is created. These electric currents are equivalent to the small circular current loops. In a magnet, these current loops are arranged parallel to each other and have currents in the same sense.
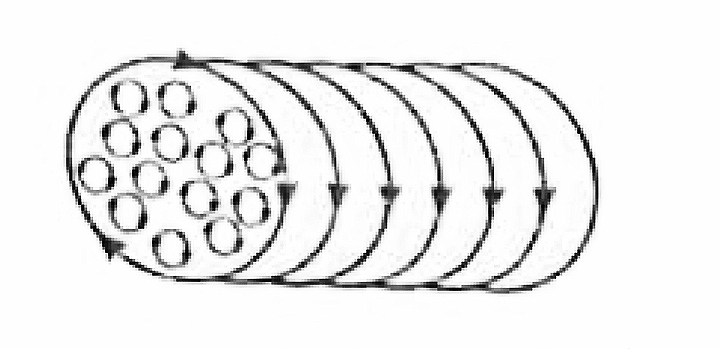
Figure 4. shows the atomic current loop in a cross-section of a cylindrical bar magnet. At any point inside the magnet, the currents from the adjacent loops cancel each other and hence net current is zero. But there is a net current on the surface. Due to this surface current, the bar magnet is equivalent to a closely wound current-carrying solenoid.
Hence, a bar magnet produces a magnetic field similar to the solenoid. It is important to note here that at the ends of the magnet, the current loops behave differently from those inside the magnet. As a result, the magnetic poles are located slightly inside the bar magnet. That is why the magnetic length of the bar magnet is slightly less than its geometrical length.
Stay tuned with Laws Of Nature for more useful and interesting content.