AMPERE’S CIRCUITAL LAW
OVERVIEW
In classical electromagnetism, Ampère’s circuital law relates the integrated magnetic field around a closed loop to the electric current passing through that loop. In 1861, James Clerk Maxwell derived it using hydrodynamics in his published paper “On Physical Lines of Force. In 1865 he generalized this equation to apply to the time-varying currents by adding the displacement current term, by adding displacement current term, it takes the modern form of the law. It is sometimes called the Ampère–Maxwell law. It is one of Maxwell’s equations that form the basis of classical electromagnetism.

In this present article, we will discuss the basics of Ampere’s circuital law and its proof, so let’s start…
AMPERE’S CIRCUITAL LAW: BASICS
Ampere’s circuital law is discovered by Andre Marie Ampere but corrected or generalized by James Clark Maxwell in 1865 by adding displacement current term.
We know that electric current in a wire creates a magnetic field in the form of concentric circles around the wire, so Ampere worked and researched on it and discovered an equation that gives the relationship between the electric current and magnetic field. This relationship is termed Ampere’s circuital law.[latexpage]

STATEMENT
This law states that the line integral of magnetic field density (B) along an imaginary closed loop called amperian loop is equal to the product of current enclosed by the loop and permeability of the medium.
Mathematically, it is given as-
$$\oint{\mathbf{B}}\cdot{d{\mathbf{l}}}=\mu_0 I$$
Alternatively, it can be also stated as the integral of magnetic H-field along an imaginary closed-loop/path is equal to the current enclosed by the path. Mathematically, it is given as-
$$
\oint{\mathbf{B}}\cdot{d{\mathbf{l}}}=\mu_0 I$$
Dividing both side by $\displaystyle{\mu_0}$, we get-
\begin{align*}
\oint\frac{\mathbf{B}}{\mu_0}\cdot d\mathbf{l}&=I\\
\implies\qquad\oint{\mathbf{H}}\cdot d{\mathbf{l}}&=I
\end{align*}
$$\left[\therefore\;\mathbf{H}=\frac{\mathbf{B}}{\mu_0}\right]
$$
AMPERE’S CIRCUITAL LAW: EXPLANATION
Let’s understand the actual meaning of Ampere’s circuital law.
Let consider a straight current-carrying conductor through which current $I$ is flowing as shown below:

Let’s mark a point P at distance r normally from the wire. Now construct a circle by taking r as a radius. This circle constitutes a surface S (surface integral) inside the circumference and this circumference is taken as a closed path C (line integral). This closed curve or path encloses the surface (S) and the electric current (which passes through the surface S).
If you take the line integral of the magnetic field around this closed curve or path C then the obtained value is equal to the $\mu_0$ times the electric current passes through the enclosed surface S.
$$
\oint{\mathbf{B}}\cdot{d{\mathbf{l}}}=\mu_0 I$$
So the integral form of Ampere’s circuital law is a line integral of the magnetic field around some closed curve C. This curve (C) encloses both a surface (S) (from which the electric current passes) and the current.
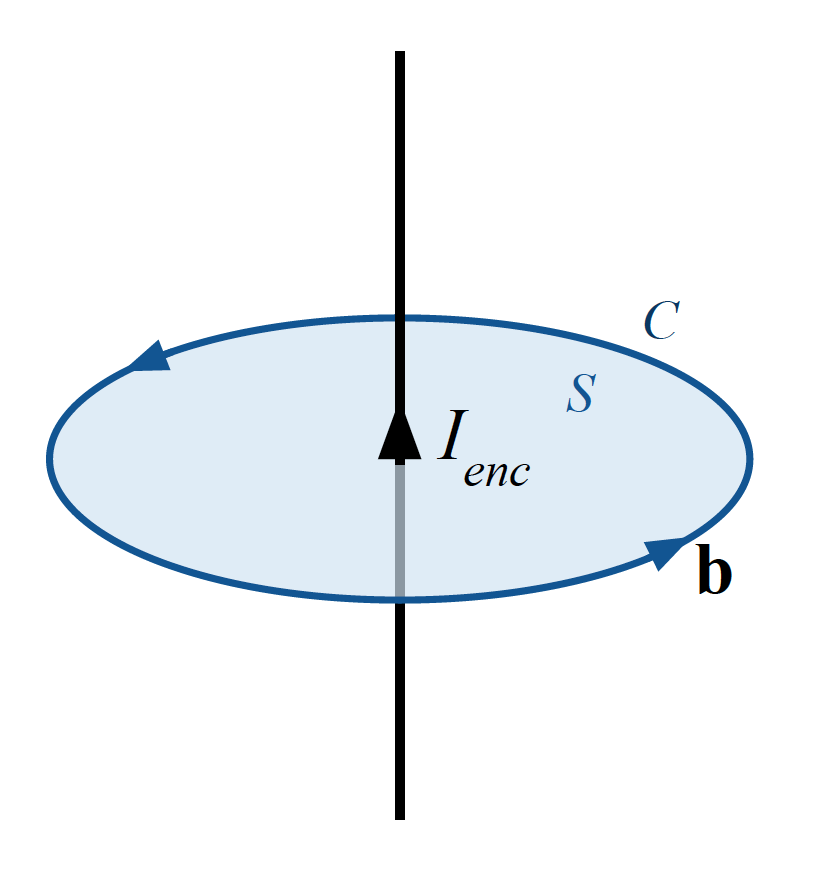
The mathematical equations of this law tell us, how the total amount of magnetic field around some path (i.e line integral) is related to the current that passes through that enclosed surface S (surface integral).
In terms of total current (i.e sum of free current and bound current) the line integral of the magnetic B-field (in terms of teslas, T) around closed curve C is proportional to the total current ($I_{encl}$) passing through the surface (S) which is enclosed by (C).
In terms of free current, the line integral of the magnetic H-field (in terms of amperes per meter, $A.m^{-1}$) around closed curve C equals the free current $I_{f, enc}$ through the surface S.
FORMS OF THE ORIGINAL CIRCUITAL LAW WRITTEN IN SI UNITS
This section will give two forms of Ampere’s circuital law, first in integral forms and second in differential forms.
When you are using magnetic B-field and total current then-
INTEGRAL FORM
| $${\displaystyle \oint _{C}\mathbf {B} \cdot \mathrm {d} {\boldsymbol {l}}=\mu _{0}\iint _{S}\mathbf {J} \cdot \mathrm {d} \mathbf {S} =\mu _{0}I_{\mathrm {enc} }}$$ |
DIFFERENTIAL FORM
| $$\displaystyle{\mathbf{\nabla}\times\mathbf{B}=\mu_0\mathbf{J}}$$ |
When you are using magnetic H-field and free current then-
INTEGRAL FORM
| $${\displaystyle \oint _{C}\mathbf {H} \cdot \mathrm {d} {\boldsymbol {l}}=\iint _{S}\mathbf {J} _{\mathrm {f} }\cdot \mathrm {d} \mathbf {S} =I_{\mathrm {f,enc} }}$$ |
DIFFERENTIAL FORM
| $$\displaystyle{\mathbf{\nabla}\times\mathbf{H}=\mu_0\mathbf{J}_f}$$ |
Where:-
- $\mathbf{J}$ is the total current density in amperes per square metre.
- $\mathbf{J}_f$ is the free current density.
- $\oint_C $ is the closed line integral around the closed curve C.
- $\iint_S$ denotes a 2-D surface integral over S enclosed by C.
- $d{\mathbf{l}}$ is an infinitesimal element.
- $d{\mathbf{S}}$ is the area vector of an infinitesimal element of surface S.
- $\nabla\times$ is the curl operator.
PROOF OF AMPERE’S CIRCUITAL LAW
Let’s take an infinitely long straight current-carrying conductor. Mark a point P at the distance r perpendicular to the conductor. Make a circle around the wire taking r as a radius. This circular closed curve (circumference) is an imaginary closed line called the Amperian loop or path. Amperian loop can be different for different structures.
This closed curve C (line integral) encloses both a surface (S) and current $I$ which is passing through the enclosed surface (S) (surface integral). Take an infinitesimal portion $d\mathbf{l}$ on the circular Amperian loop and $d\mathbf{S}$ be the area vector of the infinitesimal portion $d\mathbf{l}$ on the surface S. And also take $\mathbf{J}$ as the total current density on the surface S.
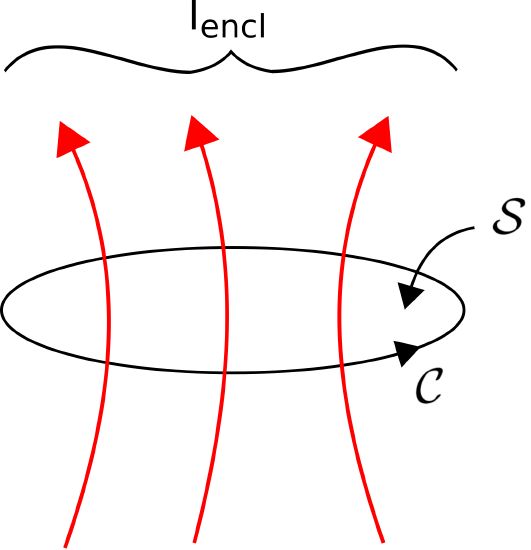
Now, from the Biot-Savart Law, we know that magnetic field at a point due to infinitely long straight current carrying conductor is given by-
$$B=\frac{\mu_0 I}{2\pi r}$$
Now transfer $2\pi r$ to the left-hand side. We get-
$$B.2\pi r=\mu_0 I$$
Now, we can write LHS in the form of integral of magnetic B-field around closed curve C (line integral) and RHS in the form of integral of current density around enclosed surface S (surface integral).
\begin{align*}
\displaystyle \oint _{C}\mathbf {B} \cdot \mathrm {d} {\boldsymbol {l}}&=\mu _{0}\iint _{S}\mathbf {J} \cdot \mathrm {d} \mathbf {S}\\
\displaystyle \oint _{C}\mathbf {B} \cdot \mathrm {d} {\boldsymbol {l}}&=\mu _{0}I_{\mathrm {enc}}
\end{align*}
This is the original integral form of Ampere’s circuital law, which we have proved by using a magnetic field due to an infinitely long straight current-carrying conductor.
We can also prove it by obtaining the value of magnetic field due to a infinitely long straight current carrying conductor at a point P placed at distance r, using Ampere’s circuital law.
IN THE FORM OF MAGNETIC B-FIELD
\begin{align*}
\oint_{C}\mathbf{B}\cdot d\mathbf{l}&=\mu_0 I\\
\mathbf{B}\oint_{C} d\mathbf{l}&=\mu_0 I\\
\mathbf{B}\cdot 2\pi r&=\mu_0 I\\
\mathbf{B}&=\frac{\mu_0 I}{2\pi r}
\end{align*}
IN THE FORM OF MAGNETIC H-FIELD
$$
\oint_{C}\mathbf{B}\cdot d\mathbf{l}=\mu_0 I
$$
Divide both side by $\mu_0$, we get-
\begin{align*}
\oint_{C} \frac{\mathbf{B}}{\mu_0}\cdot d\mathbf{l}&=I\\
\oint_{C} \mathbf{H}\cdot d\mathbf{l}&=I\\
\mathbf{H}\oint_{C} d\mathbf{l}&=I\\
\mathbf{H}\cdot 2\pi r&=I\\
\mathbf{H}&=\frac{I}{2\pi r}
\end{align*}
This is the same magnetic field, which we have derived using Biot-Savart Law in previous articles for infinitely long straight current carrying conductor. So this is the required proof of Ampere’s circuital law.
AMPERE’S CIRCUITAL LAW IN CGS UNITS
Ampere’s circuital law in CGS units with Maxwell’s correction is given below:
IN INTEGRAL FORM
| $${\displaystyle \oint _{C}\mathbf {B} \cdot \mathrm {d} {\boldsymbol {l}}={\frac {1}{c}}\iint _{S}\left(4\pi \mathbf {J} +{\frac {\partial \mathbf {E} }{\partial t}}\right)\cdot \mathrm {d} \mathbf {S} }$$ |
Where c is the speed of light.
IN DIFFERENTIAL FORM
| $${\displaystyle \mathbf {\nabla } \times \mathbf {B} ={\frac {1}{c}}\left(4\pi \mathbf {J} +{\frac {\partial \mathbf {E} }{\partial t}}\right)}$$ |
APPLICATIONS OF AMPERE’S CIRCUITAL LAW
Some applications of Ampere’s circuital law is listed below:
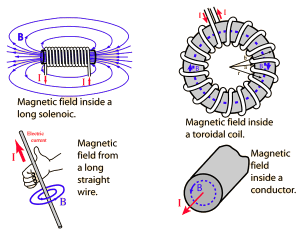
- It is used to find the magnetic field of complex structures.
- It is used to find the magnetic field due to an infinitely long straight current-carrying conductor.
- It is used to find the magnetic field due to the long current carrying conducting cylinder.
- It is used to find the magnetic field due to the long current carrying conducting hollow cylinder.
- It is used to find the magnetic field due to a solenoid.
- It is used to find the magnetic field due to a toroid.
Stay tuned with Laws Of Nature for more useful and interesting content.