In this article, we will discuss, an AC circuit that contains a capacitor only. So let’s get started…
AC circuit containing a capacitor only
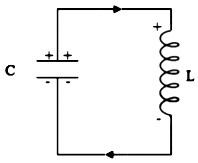
Consider an AC circuit containing a capacitor of capacitance $C$ connected across an alternating voltage source of EMF $\mathcal{E}$ given by $$\mathcal{E}=\mathcal{E_0}\sin\omega t\qquad ….(1)$$
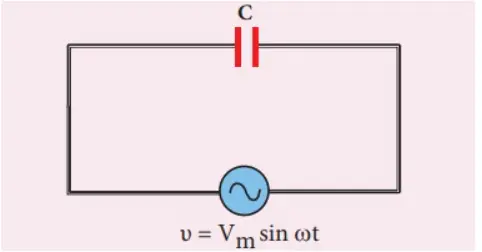
Due to the continuous changing and discharging of the capacitor plates, a constant but alternating current exists in the circuit. At any instant.
P.D. across the capacitor plates $=$ Applied emf i.e. $$V=\mathcal{E}=\mathcal{E_0} \sin \omega t$$But $\quad V=\frac{Q}{C}$ or $\qquad\mathrm{Q}=\mathrm{CV}=\mathrm{C\mathcal{E_0}} \sin \omega t$
$\therefore$ Current at any instant is
$$I=\frac{d Q}{d t}=\frac{d}{d t}\left(C \mathcal{E_0} \sin \omega t\right)=\omega C\mathcal{E_0} \cos \omega t$$or$$
I=I_0 \cos \omega t=I_0 \sin (\omega t+\pi / 2)\quad … (2)$$ Where $I_0=\omega C \mathcal{E_0}=\frac{\mathcal{E_0}}{1 / \omega C}=$ the current amplitude.
Phase relationship between $ \mathcal{E}$ and $I$
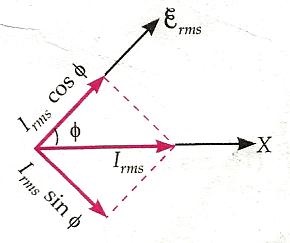
Comparing equations (1) and (2), we can find that in a capacitive AC circuit, the current leads to the voltage or voltage lags behind the current in phase by $\pi/2$ radian. The phase relationship between $\mathcal{E}$ and $I$is shown graphically below the right side image. We see that the current reaches its maximum value earlier than the voltage by one-fourth of a period.
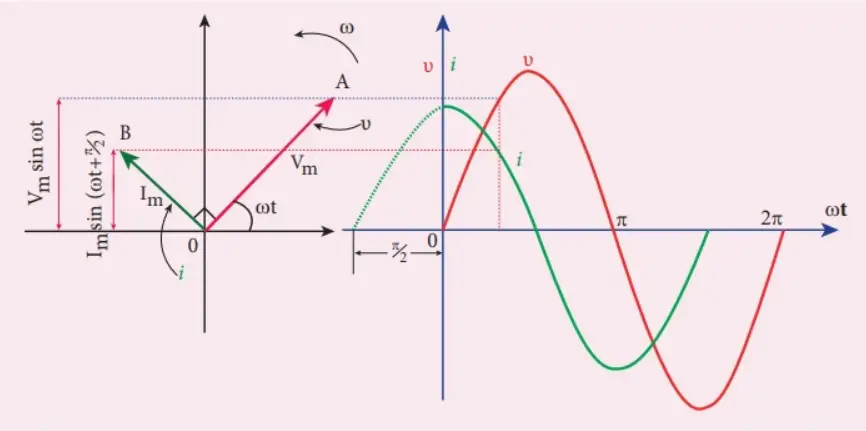
The left part of the image shows the phasor diagram for a capacitive AC circuit. The phasor $\overrightarrow{\mathcal{E}}$ makes an angle $\omega t$ with X-axis in the anti-clockwise direction. As the current leads the voltage in phase by $\pi/2$ rad, so the current phase $\overrightarrow{I}$ makes an angle $\pi/2$ rad with the phase $\overrightarrow{\mathcal{E}}$ in the anti-clockwise direction.
Read Also
- Phasor and phasor diagram class 12
- Derive an expression for the average or mean value of AC for half cycle
- Expression for the RMS value of alternating current for a full cycle
Capacitive reactance
Comparing the relation, $\displaystyle{I_0 =\frac{\mathcal{E_0}}{1 / \omega C}}$ with the ohmic relation $\displaystyle{I_0=\frac{\mathcal{E_0}}{R}}$, we find that the factor $\displaystyle{\frac{1}{\omega C}}$ is the effective resistance or opposition offered by the capacitor to the flow of AC.
This effective resistance or opposition offered by the capacitor to the flow of AC is called capacitive reactance and is denoted by $X_C$.
Thus $X_C=\frac{1}{\omega C}=\frac{1}{2 \pi f C}$
The $\mathrm{SI}$ unit of capacitive reactance is ohm $(\Omega)$.
For AC, $X_C \propto \frac{1}{f}$
For DC, $f=0 \quad \therefore X_C=\infty$
Thus a capacitor allows AC to flow through it easily but offers infinite resistance to the flow of DC., i.e, a capacitor blocks DC Obviously,
$$I_{r m s}=\frac{I_0}{\sqrt{2}}=\frac{\mathcal{E_0}}{1 / \omega C \cdot \sqrt{2}}=\frac{\mathcal{E}{r m s}}{1 / \omega C}=\frac{\mathcal{E}_{r m s}}{X_C}$$
Variation of capacitive reactance with frequency
Capacitive reactance, \begin{aligned}X_C&=\frac{1}{\omega C}=\frac{1}{2 \pi f C}\\i.e., \qquad X_C \propto & \frac{1}{f}\end{aligned}
Thus the capacitive reactance varies inversely with the frequency. As $f$ increases, $X_C$ decreases. The below figure shows the variation of $X_C$ with $f$.
Read Also
- AC circuit containing resistor only, class 12
- AC circuit containing an inductor only
- Representation of AC current and voltage by phasor diagram
Effect of a capacitor in an AC circuit
The below figure shows a capacitor of capacitance $C$ is connected to alternating EMF. Due to the alternating voltage of the source, the capacitor gets charged in one direction in the first half cycle, then discharged, and then charged in the opposite direction during the second half cycle and again discharged, and so on.

As a result, there is a continuous flow of alternating circuits. Thus, a capacitor provides an easy alternating current (AC) path.
Frequently Asked Questions – FAQs
What is a capacitor?
A capacitor is a device that stores electrical energy in an electric field. It is a passive electronic component with two terminals.
What is capacitive reactance?
The effective resistance or opposition offered by the capacitor to the flow of AC is called capacitive reactance and is denoted by $X_C$.
What is the formula for capacitive reactance?
The formula of capacitive reactance is $X_C=\frac{1}{\omega C}=\frac{1}{2 \pi f C}$
What happens to capacitors in AC circuits?
Once the capacitor is “fully charged,” it blocks the flow of more electrons onto its plates when they become saturated. However, when we apply an AC or AC power supply, the capacitor will alternately charge and discharge at a rate determined by the frequency of the supply.
How does capacitive reactance vary wrt frequency?
The capacitive reactance varies inversely with the frequency.
Stay tuned with Laws Of Nature for more useful and interesting content.